Untersuche die Funktion f auf ihr Monotonieverhalten?
Ich habe in Mathe heute eine Aufgabe bekommen und Verstehe gar nichts.
Unterusche die Funktion f auf ihr Monotonieverhalten
a) f(x)= 2x³-24x
b) f(x)=-3x²4x
5 Antworten
Das Monotonieverhalten kannst du mit der ersten Ableitung bestimmen.
Dabei musst du die erste Ableitung größer Null und kleiner Null setzen.
Denn wo f' positiv ist da ist f monoton steigent und wo f' negativ da ist f monoton fallend.
f'(x)=6x²-24
6x²-24>0 x²>4. x> +- 2
D.h. x ist größer Null für x > größer +- 2
D.h. der Graph von f ist im Intervall
]Unendlich ; -2] U [+2 ; Unendlich[
Monoton steigent. Der rote Graph ist die Ableitung.
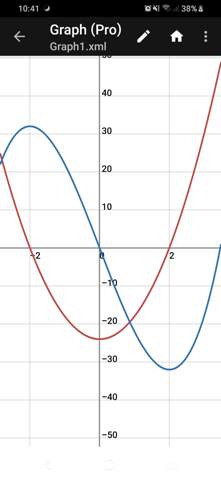
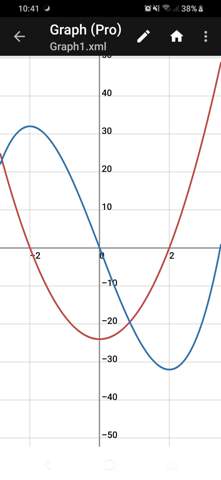
Ich hab ein Fehler gemacht die -2 und zwei sind nicht eingeschlossen weil die steigung dort null ist.
Also dss intervall ist
] -unendlich ; -2[ U ]2 ; +unendlich[
Hallo, deine Aufgabe ist ansich recht einfach zu verstehen
I) lokale Extrema bestimmen über NB und HB
f(x)= 2x³-24x
f'(x) =6x^2-24
f(x)=-3x²4x
f'(x) =-6x-4
Nullstellen von f'(x) bestimmen
Für das Monotonieverhalten machst du eine Vorzeichentabelle
Angenommen x sei0 und 2 dann untersucht du den Verlauf der Ableitung bzw den Vorzeichenwechsel in Intervallen
I1 Kann sein - unendlich bis zur Nullstelle1
I2 Nullstelle1 bis Nullstelle2
I3 Nullstelle 2 bis +unendlich
Um das Monotonieverhalten bei unendlich zu ermitteln setzt du bei - unendlich eine negative Zahl ein die unter der Nullstelle liegt bei +unedlich umgekehrt
Wenn du das Monotonieverhalten dann aufschreiben bzw interpretieren willst gilt
f'(x) <0 monoton fallend
f'(x) >0 Monoton wachsend /steigend
Schreib am Ende aber immer die Intervalle dazu
Formulierung :f ist im Intervall 1(Klammern beachten) monoton steigend, da f'(x) >0 ist
Du musst die hochpunkte / Tiefpunkte / sattelpunkte herausfinden.
( 1. Ableitung = 0)
und dann überprüfst du die Steigung links und rechst von den Punkten .
je nachdem was für ein Punkt du hattest ist es dan in dem Intervall streng monoton steigend oder fallend .
befindet sich ein sattelpunkt in deinem Intervall dann ist die Funktion nicht mehr streng monoton fallend oder steigend sondern nur noch monoton
Bsp :
f‘(x) = 6x^2 - 24
0 = 6x^2 - 24
-x^2 =- 4
x = 2
dirsf Funktion hat also nur einen Tiefpunkt .
das heißt das die Funktion von - unendlich bis x= 2 streng monoton fällt . Und von 2 bis unendlich streng monoton steigt .
Ähm falsch sie hat natürlich bei x= -2 auch einen Hochpunkt
also ist ihr Monotonie verhalten :
von - unendlich bis -2 streng monoton steigend.
von -2 bis 2 streng monoton fallen
von 2 bis unendlich streng monoton steigend
sry 😅
Bilde die Ableitung und bestimme dann die Nullstellen der Ableitung. Falls sie einfache nullstellen hat, ist die Funktion nicht monoton
Hi,
welche Klasse?
Kennst Du Ableitungen?
LG,
Heni
also die Ableitung bei a ist somit:
6x² - 24
Diese setzen wir gleeich null und bestimmen auf welchen Intervalen sie positiv und auf welcheen negativ ist:
6x² - 24 = 0 | :6
x² = 4 | √
x1 = -2
x2 = 2
wenn a > 0: ist die Funktion 2. Grades zwischen den Nullstellen negativ, und außerhaöb derer positiv.
wenn a<0 ist die Funktion 2. Grades zwischen den Nullstellen positiv, und außerhaöb derer negativ.
a ist der Koefizient der vor x² steht, in unserem Fall ist a =1, also a>0, glit also die Regel für a > 0,
Da wo die Ableitung positiv ist, ist der Graph der Funktion streng monoton steigend und wo die Ableitung negativ ist, ist der Graph der Funktion streng monoton fallend.
also für x € (-∞ : - 2) U ( 2 : + ∞) ist diese montoton steigend
und auf dem Interval ( -2 : 2) ist sie monoton fallend
10 Klasse und Ableitungen kenne ich und habe die auch bereits gebildet, aber ich weiß nicht wie ich dann weiter machen muss