Was ist der Unterschied zwischen klassischer und moderner Physik?
Kann mir das jemand in einfachen Worten erklären? Danke :).
4 Antworten
Der größte Unterschied ist vermutlich der Determinismus.
In der klassischen Physik glaubte man, man könnte alles genau berechnen, wenn man nur alle Daten zur Verfügung stehen hätte und dass alles genau einen Zustand annehmen würde.
Die moderen Physik und gerade die Quantenphysik arbeitet aber mit dem Suoerpositionsprinzip. D.h. dass sich auch Zustände überlagern können.
Man hat außerdem durch die Heisenberg'sche Unschärfebeziehung keine genaue Bestimmung mehr von Ort und Impuls sowie Zeit und Energie gleichzeitig mit beliebiger Genauigkeit.
Das Gegenteil von "klassisch" ist hier nicht "modern"!
Sondern "relativistisch" bzw. "quantenmechanisch".
Auch moderne Physik kann klassisch sein.
Nicht-klassiche Physik benutzt weitergehende Grundlagen, die bei "makroskopischer" Physik keine Rolle spielen oder nicht berücksichtigt werden müssen, und Instrumente, welche weit über die menschlichen Sinne hinausgehen.
Es ist eine Art Tradition, die Klassische Physik als „das Alte“ und die neuen Theorien ab 1900 (Relativitätstheorie und Quantentheorie) als Revolutionen anzusehen, die dieses „Alte“ quasi vom Sockel gestoßen hätte.
Überzeugender ist es freilich m.E., gerade die Relativitätstheorie der klassischen Physik, auf deren Prinzipien sie vollständig basiert, zuzurechnen. Die Quantentheorie wiederum bringt schon noch etwas radikal Neues ins Spiel, nämlich das Wirkungsquantum und die Tatsache, dass Teilchen generell auch Wellen sind.
Statt „den Unterschied zwischn klassischer und moderner Physik“ aufzuzeigen, will ich lieber aufzeigen, was Klassische Physik historisch ist, und dann auf die Theorien der letzten 120 Jahre zu sprechen zu kommen.
Vorklassische NaturphilosophieIm Altertum waren die Naturwissenschaften weit weniger systematisch als heute und als Naturphilosophie Teil der Philosophie. Die Erde wurde als ruhendes Zentrum des Kosmos angesehen, wobei sie im späteren Verlauf schon als annähernd kugelförmig galt.
Eine wichtige Rolle in der Naturphilosohpie spielt Aristoteles (384-322v.Chr.), der u.a. glaubte, dass es für verschiedene Bereiche (z.B. Erde und außerirdischer Kosmos) unterschiedliche Gesetze gebe, wobei zu den irdischen gehöre, dass eine Kraft erforderlich sei, um Bewegung hervorzurufen oder aufrecht zu erhalten.
Diese Idee wurde später u.a. von Ibn Sina (um 980 bis um 1037, ab hier n.Chr.) durch die Impetustheorie modifiziert, mit der auch Würfe und Schüsse erklärt werden sollten. Das Wort „Theorie“ täuscht allerdings darüber hinweg, dass sie längst nicht so systematisch ausgearbeitet war wie spätere Theorien.
Im Mittelalter und der frühen Neuzeit blieb Aristoteles trotz weiterer Fortschritte lange die Autorität schlechthin.
Die klassische RevolutionDas änderte sich mit dem Wirken Galilei Galileis (1564-1642), der als Astronom ein Anhänger des neuen heliozentrischen Weltbildes war, das Nikolaus Kopernikus (1473-1543) vorgeschlagen hatte. Er stellte im Laufe seines Lebens zwei wichtige Prinzipien der Physik auf:
- Trägheitsprinzip: Kraft ist erforderlich, um den Bewegungszustand zu ändern. um den Ein Körper, auf den netto keine Kraft wirkt, bewegt sich geradlinig-gleichförmig (oder gar nicht), er hat eine konstante Geschwindigkeit |v› (die auch 0 sein kann).
- Relativitätsprinzip (RP): Naturgesetze, also die grundlegenden Beziehungen zwischen physikalischen Größen, sind unabhängig davon, auf welches Koordinatensystem die Größen selbst bezogen werden. Mit rein physikalischen Methoden lässt sich also nicht eine Geschwindigkeit an sich ermitteln.
Gerade das RP kann sehr gut erklären, wie sich die Erde immer schon bewegen konnte, ohne dass dies jemand merkte.
Kein Name ist mit der Klassischen Revolution enger verbunden als der Isaac Newtons (1643-1727), der die Bewegung der Himmelskörper auf dieselbe Kraft zurückführte, die auch Dinge fallen lässt: Das Gesetz der allgemeinen Massenanziehung.
Zudem formulierte er das
- Wechselwirkungsprinzip: Übt ein Körper B₁ auf einen anderen Körper B₂ die Kraft |F›₁₂ aus, so übt auch B₂ auf B₁ eine gleich starke, entgegengesetzt gerichtete Kraft |F›₂₁=–|F›₁₂ aus.
Dieses Prinzip ist äquivalent zum Impulserhaltungssatz. Ihm verwandt ist auch der Drehimpulserhaltungssatz, dessen Anwendung auf die Planetenbewegung auch als das zweite Gesetz von Johannes Kepler (1571-1630) bekannt ist.
Auf Newton geht auch die Formel
(1) |F› = m·|a› (Kraft gleich Masse mal Beschleunigung)
zurück. Später formulierte Julius Robert von Mayer (1814-1878) den Energieerhaltungssatz, auf den er kam, indem er die bei mechanischen Vorgängen abgegebene Wärme mit der mechanischen Arbeit verglich.
Auf der Grundlage der theoretischen Arbeiten von (unter anderem) Joseph Lagrange (1736-1813) und William Rowan Hamilton (1805-1865) konnte Emmy Noether (1882-1935) die Erhaltungssätze auf grundlegende Symmetrien des Kosmos (genauer gesagt, der sogenannten Wirkung) zurückführen.
----
Elektrodynamik Ein riesiger Teil der Klassischen Physik ist die von James Clerk Maxwell (1831-1879) formulierte Elektrodynamik. Maxwell konnte auch die Existenz elektromagnetischer Wellen voraussagen, die sich durch den materiefreien Raum mit einem bestimmten Tempo ausbreiten, das sich allein aus den Grundkonstanten der Elektrodynamik ergibt.
Dieses Tempo ist die Lichtgeschwindigkeit c, und Licht besteht aus elelektromagnetischen Wellen. Dass sie sich mit c ausbreiten, ist also im Grunde auch ein Naturgesetz.
Experimentell wurden elektromagnetische Wellen geringerer Frequenz als Licht - die auch eindeutig als elektromagnetische Wellen erkennbar waren - durch Heinrich Hertz (-1884) erzeugt.
Spezielle Relativitätstheorie (SRT)Die Spezielle Relativitätstheorie beruht auf der Elektrodynamik, was sich schon am Titel von Albert Einsteins (1879-1955) Aufsatz „Elektrodynamik bewegter Körper“ von 1905 zeigt. Genauer gesagt ist sie die konsequente Anwendung des Relativitätsprinzips auf die Elektrodynamik.
Das heißt konkret, dass etwas, das sich in einem Koordinatensystem Σ mit c bewegt, dies auch in einem relativ dazu bewegten System Σ′ mit c bewegt, was dazu führt, dass die Zeit untrennbar mit den Raumdimensionen verbunden ist zur Raumzeit, in der es zwischen zwei Ereignissen ein absolutes Abstandsquadrat
(2.1) c²Δτ² := c²Δt² – ‹Δr|Δr› ≡ c²Δt′² – ‹Δr′|Δr′›
gibt. Dabei ist Δt eine Zeitspanne und sind
(2.2) ‹Δr|Δr› = Δx² + Δy² + Δz² bzw. ‹Δr′|Δr′› = Δx′² + Δy′² + Δz′²
das räumliche Abstandsquadrat in Σ bzw. Σ′. Die durch (2.1) gegebene Metrik (Maß für Entfernungen) ist nach Einsteins Lehrer Hermann Minkowski (1864-1909) benannt. Geht man von eng benachbarten Ereignissen aus, kann man wahlweise kartesische Koordinaten oder Polarkoordinaten verwenden:
(2.3) ‹dr|dr› = dx² + dy² + dz² = dr² + r²dθ² + r²sin²(θ)dφ
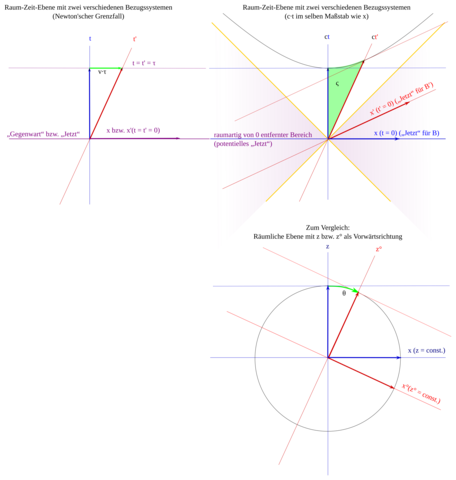
Das Minuszeichen in (2.1) sorgt für eine wichtige Unterscheidung in einen zeitartigen (c²Δτ²>0), lichtartigen (c²Δτ²=0) und raumartigen (c²Δτ²<0) Abstand zwischen zwei Ereignissen und macht somit einen wichtigen Unterschied zwischen Zeit und Raum (s. Schaubild).
Überlegungen zum Impulserhaltungssatz führen zu der Erkenntnis, dass eigentlich Masse und Energie keine zwei voneinander zu trennenden Größen sein können, sondern Masse sozusagen kondensierte Energie darstellt und Energie träge und schwer ist. Nichts anderes sagt die berühmte Formel
E = mc²
aus. Energie und Impuls lassen sich zum sog. Viererimpuls
(3.1) |p» := (E/c ¦ |p›)
mit dem „Betrag“
(3.2) √{E²/c² – ‹p|p›} = √{E²/c² – p²} = mc
zusammenfassen.
Der Speziellen Relativitätstheorie fällt vor allem Newtons „Dogma“ von der „absoluten, mathematischen Zeit“ zum Opfer. Diese Hypothese hat Newton aber für seine Physik gar nicht gebraucht. Wenn man Einstein als „Revolutionär“ bezeichnen will, dann nicht gegen Galilei, sondern als dessen Erbe und Fortsetzer seiner Revolution gegen überkommene Vorstellungen, respektive deren Überreste innerhalb der klassischen Physik.
Allgemeine RelativitätstheorieSie beruht auf dem Äquivalenzprinzip. Der Ursprung dessen geht auch noch auf Galilei zurück, der erkannte, dass im Prinzip alle Körper gleich schnell fallen (würden, wenn es keinen Luftwiderstand gäbe).
Die Gravitation ist die einzige Kraft, die zur Masse proportional ist, was sie mit den Trägheitskräften gemeinsam hat. Somit besagt das Äquivalenzprinzip, dass eine Situation unter Einfluss eines homogenen Gravitationsfeldes und unter dem einer gleichförmigen Beschleunigung experimentalphysikalisch nicht unterscheidbar sind. Außerdem reagiert jede Energie auf Gravitation, auch Licht.
Das führt u.a. dazu, dass Zeitspannen und räumliche Distanzen vom Gravitationspotential abhängen. Nun sind auch Gravitationsfelder im Allgemeinen nicht homogen. Alles in allem führt das zu der Möglichkeit, ein Gravitationsfeld als Krümmung der Raumzeit zu beschreiben.
Die üblichen Bilder von Dellen in einem Gummituch, in denen Murmeln in Mulden rollen, solltet Du allerdings am besten vergessen. Sie „erklären“ Gravitation mit Gravitation, nämlich der der Erde unter dem Tuch. Die Murmeln folgen keinesfalls der Krümmung, sondern würden beispielsweise, wenn die Mulde eine Wölbung wäre, nach außen rollen.
Eine Ameise mit der Fähigkeit, genau geradeaus zu laufen, würde vermutlich auch von einer Wölbung nach oben nach innen hin abgelenkt. Sie folgt also der Krümmung. Allerdings hat Krümmung der Raumzeit nichts mit Krümmung in einem höherdimensionalen Raum zu tun, sondern ist eine innere Geometrieeigenschaft.
Dass Krümmung einer Fläche sich ohne Referenz auf eine Einbettung in einen höherdimensionalen Raum verstehen lässt, ist eine Erkenntnis, die auf Carl Friedrich Gauß (1777-1855) zurückgeht. Er nannte dies Theorema Egregium.
Dieses Konzept wurde von Bernhard Riemann (1826-1866) auf eine sog. Mannigfaltigkeit (Verallgemeinerung einer Fläche) höherer Dimension verallgemeinert und von Einstein schließlich auf die oben erwähnte Raumzeit angewandt.
So wird zum Beispiel die Raumzeit in der Nähe einer Punktmasse (ist natürlicheine Idealisierung) am Ursprung r=0 durch die von Karl Schwarzschild (1873-1916) gefundene Metrik
(4) c²dτ² = c²dt²(1 – r.S/r) – [dr²/(1 – r.S/r) + r²dθ² + r²sin²(θ)dφ]
beschrieben, wobei r.S der Schwarzschild-Radius heißt und r zwar noch eine „Umkugel“ mit der Fläche 4πr² um den Ursprung, aber dank der Verzerrung nicht mehr der räumliche Abstand vom Ursprung ist. Die Fläche r=r.S markiert einen sogenannten Ereignishorizont, falls der Körper tatsächlich keinen größeren Radius als r.S hat. In so einem Fall spricht man seit den 1960er Jahren von einem Schwarzen Loch.
Die quantische RevolutionAllen Gebieten der klassischen Physik ist gemeinsam, dass sie klar zwischen Körpern bzw. Teilchen einerseits und Feldern bzw. Wellen andererseits unterscheiden.
Diese Trennung erwies sich als nicht haltbar, und darin liegt das Neue an der Quantentheorie.
Sie bröckelt schon mit der Erkenntnis, dass es Wellen ohne materiellen Träger gibt (Licht zum Beispiel). Diese Wellen sind elektromagnetische Wechselfelder.
Und die bestehen aus „Portionen“ der Energie h·f, wobei f die Frequenz ist und h (wie „Hilfsgröße“) das 1900 von Max Planck (1858-1947) eingeführte Wirkungsquantum ist.
Planck hielt dieser Quantelung nicht unbedingt für eine Eigenschaft des Lichts selbst, doch Einstein konnte die Idee 5 Jahre später bestens zur Erklärung des Photoelektrischen Effekts gebrauchen: Licht kann unter gewissen Bedingungen Elektronen aus Metall schlagen und damit einen Strom auslösen. Das tut es aber erst ab einer bestimmten Frequenz, darunter löst es keinen Photostrom aus, egal wie hell es ist.
Man stelle sich einen Ball in einer Kuhle vor. Tritt man fest genug dagegen, fliegt er raus. Ist der Tritt nicht fest genug, geschieht das nicht, selbst wenn man durch hunderte von Tritten insgesamt deutlich mehr Energie aufwendet - sie verpufft. Der Tritt entspricht dem Photon.
Dass umgekehrt Materieteilchen auch Wellen sind, postulierte erstmals Louis de Broglie (1892-1987) im Rahmen seiner Doktorarbeit von 1924. Dieses Wellenmodell erklärt auf ganz natürliche Weise die 1913 von Niels Bohr (1892-1962) ad hoc postulierten gequantelten Energiezustände eines Elektrons im Atom: Das Elektron muss eine Art stehende Welle bilden.
Zugleich liefert es eine natürliche Erklärung für die von Werner Heisenberg (1901-1976) formulierte Unschärferelation, auch wenn dieser sie abstrakter begründet hat, mit der sogenannten Matrizenmechanik, welche die Zustände von Atomen mit Mitteln der Linearen Algebra beschreibt.
1926 zeigte Erwin Schrödinger (1887-1961), dass die Wellenmechanik und die Matrizenmechanik gleichwertig sind, und entwickelte eine Gleichung für den Newton-Limes (v≪c).
Diese Gleichung wurde von Wolfgang Pauli (1900-1958) erweitert, um das Konzept des Spin einzubinden, einer Eigenschaft, die dem Drehimpuls eines Kreisels ähnliche Eigenschaften hat, aber viel abstrakter ist.
1928 entwickelte Paul Dirac (1902-1984) unter Einbindung von Paulis Formalismus und einer zuvor von Oskar Klein (1894-1977) und Walter Gordon (1893-1939) entwickelten Gleichung, die die Relativitätstheorie berücksichtigt, eine detailliertere, auf z.B. das Elektron anwendbare Gleichung, die dies auch tut und dabei automatisch den Spin vorhersagt.
Sie enthält Paulis Gleichung als Grenzfall.
Die „relativistischen“ Wellengleichungen der Quantenmechanik sagen auch die Existenz von Antiteilchen zu jedem Teilchen voraus.
Durch Beugung von Elektronen an Kristallen war es 1927 Clinton Davisson (1881-1958) und Lester Herbert Germer (1896-1971) gelungen, dessen Wellennatur nachzuweisen.
Erst die Quantentheorie konnte die chemischen Eigenschaften von Materie auf die Physik zurückführen.
Meist wird die Grenze bei der Einsteinschen Relativitätstheorie und der Quantentheorie gezogen - "klassische" Physik ist alles, was diese Theorien nicht berücksichtigt.
Selten wird die Grenze auch bei anderen einschneidenden Theorien gezogen - z. B. zwischen Spezieller und Allgemeiner Relativitätstheorie, oder in historischen Betrachtungen bei Heranziehung des Experiments (und allgemeiner der sorgfältigen Beobachtung mit nicht vorweggenommenem Ergebnis) bei Galilei.
Von der Dichotomie „klassisch versus relativistisch“ halte ich nichts.
Die Relativitätstheorie beruht nämlich gerade auf den Prinzipien der Klassischen Physik, namentlich Galileis Relativitätsprinzip, das Einstein im Grunde nur noch auf die Gesetze der Elektrodynamik anwenden musste.
Die vor der Relativitätstheorie oft favorisierte Hypothese des absolut ruhenden Äthers ist im Grunde gar keine klassische Physik, weil ihr das Relativitätsprinzip fehlt.