Wie muss x gewählt werden, damit die Fläche der rechteckigen Platte möglichst groß wird?
Hei zusammen, komme bei folgender Frage nicht weiter:
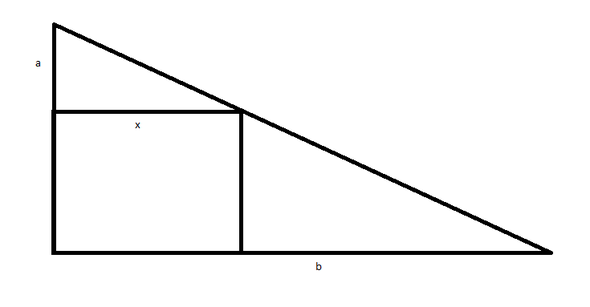
Aus einer dreieckigen Steinplatte mit a=0.4m und b=0.6m soll ein Rechteck mit der Länge x herausgesägt werden. Wie muss x gewählt werden, damit die Fläche der rechteckigen Platte möglichst gross wird?
Kann mir da jemand weiter helfen?
Update: Vielen Dank euch allen für die zahlreichen und schnellen Antworten, das mit dem Strahlensatz ist mir auch bereits im Kopf rumgeschwirrt, nur wusste ich nicht genau wie ich ihn anwenden muss, werde es morgen nochmals probieren.
Gruss Orangeray
6 Antworten
Die Analytische Geometrie hilft uns weiter:
Sagen wir, das sei eine lineare Funktion in einem Intervall, so wäre die Funktionsgleichung f(t)=-a/bx+a, jetzt müssen wir darunter ein Rechteck bekommen also nehmen wir einen Wert und multipliezieren ihn mit seinem Funktionswert: (-a/bt+a)*t=-a/bt^2+at, jetzt müssen wir das Maximum dieser neuen Funktion finden, dies tun wir indem wir die erste Ableitung gleich 0 setzten: -2a/bt+a=0 durch Äquivalenzumformungen bekommen wir t=b/2, also ist das rechteckt b/2*f(b/2)=b/2*(-a/2+a)=b/2*a/2=ab/4.
x wäre demnach am besten bei b/2=0.3m gewählt.
Ich hoffe, ich konnte helfen;)
Die beste Strategie dürfte sein: durch die Eckpunkte der Steinplatte eine (lineare) Funktion legen. Dann liegt der rechte obere Punkt des Rechtecks auf dem Graphen dieser Funktion.
Zielfunktion: Fläche eines Rechtecks. Breite ist bekannt; Höhe ist der y-Wert Deiner linearen Funktion an der Stelle x.
Soweit meine Hilfestellung.- Nun kommst Du :-)
Zunächst: Was muss maximal werden?
Maximal muss der Flächeninhalt A werden.
A = x*y
nun die Frage: Wie hängen x und y voneinander ab?
Klar ist, wenn du y größer machst, wird y kleiner.Schwierig ist nur das verhältnis. Dazu kannst du dir vorstellen, dass du das ganze mal in einem Koordinatensystem betrachtest. der Ursprung (0I0) sollte nun mal bei deiner Zeichnung links unten sein (am rechten Winkel).
Jetzt pberleg dir die Formel für die Diagonale:
y=m*x + n, wobei n (Der y-Achsenabschnitt) hier durch a gegeben ist (0,4)
m ist die Steigung, die kannst du dir ausrechnen (m = 0,6 / -0,4 = -3/2)
Damit gilt: y= -3/2x+0,4
Einsetzen in die erste Formel ergibt A = -3/2 *x² + 0,4x
Nun Ableiten: A' = -3*x+0,4
Für den Extremwert brauchen wir die Nullstelle:
0 = -3*x+0,4 <=>
3x = 0,4 <=>
x=2/15
Nun kannst du y ausrechnen: y= 0,2
NACHRECHNEN! kann sein, das ich beim Kopfrechnen Fehler gemacht habe.
Anmerkung: Theoretisch musst du bei den Extremstellen die Ränder noch überprüfen
Strahlensatz: y / (b - x) = a / b → y = (a/b) (b - x)
Rechteckfläche A = x y = (a/b) (bx - x²)
A'(x) = (a/b) (b - 2x)
A'(x) = 0 → 2x = b usw.
Das hatten wir doch vor 3 Wochen schon einmal. Hier die gleiche Antwort wie beim letzten mal:
Wenn du ein wenig nachdenkst, brauchst du gar nichts rechnen.
Dies ist eine Extremwertaufgabe, die letztendlich auf eine quadratische Funktion hinausläuft.
Offensichlich hat diese zwei reelle Nullstellen. Einmal am linken Rand bei x=0m und ein zweites mal am rechten Rand bei x=b=0.6m. Für jedes x, das zwischen den beiden Nullstellen, liegt ist die Fläche des gesuchten Rechteckes größer als Null. Und irgendwo gibt es ein Maximum - und zwar genau eins. Das haben quadratische Funktionen so an sich.
Was quadratische Fuhktion noch so an sich haben ist allerdings die Tatsache, daß:
Wenn eine quadratische Funktion zwei reelle voneinander verschiedene Nullstellen hat, dann liegt das Extremum immer und zwar wirklich immer genau in der Mitte zwischen den beiden Nullstellen.
Da hast du deine Lösung - ohne zu Rechnen ;-)