Mindestgeschwindigkeit vx?
Folgende Herausforderung stellt sich mir gerade in Physik. Ich würde mich über Unterstützung sehr freuen.
Zwei jeweils die positive Ladung Q = 2 · 10-9 As tragende Kugeln sind so aufgestellt, dass zwischen ihren Mittelpunkten ein Abstand d = 12 cm besteht. Aus sehr großer Entfernung soll ein Elektron genau zwischen ihnen hindurch geschossen werden.
a)Erläutern Sie die Bedeutung des Hinweises „… aus sehr großer Entfernung …“ für diese Aufgabenstellung!
b)Berechnen Sie die Mindestgeschwindigkeit vx, die dem Elektron hierzu erteilt werden muss!
c)Entscheiden Sie, ob das von Ihnen errechnete Ergebnis physikalisch möglich ist!“
Für Aufgabe a) ist das meine Lösung:
a) Dies muss so verstanden werden, als käme das Elektron „aus dem Unendlichen“. Daher ist das Startpotenzial gleich Null.
Ergänzung

Ich würde die Formel verwenden aber wie komme ich auf rB und rA ?
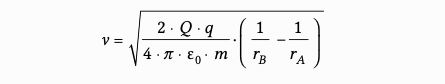
1 Antwort
Das negativ geladene Elektron erfährt durch die positiven Ladungen eine Anziehung. Warum sollte eine Mindestgeschwindigkeit erforderlich sein, um dorthin zu gelangen?
Wären die Ladungen negativ, würde das Beispiel für mich mehr Sinn machen.
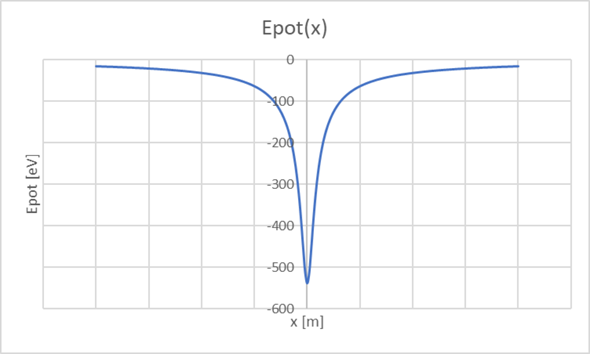
Wenn die beiden Ladungen nämlich positiv sind, wird die potenzielle Energie des Elektrons bei Annäherung kleiner (Anziehung). Nun kann man für unendliche Entfernung die potenzielle Energie Null setzen, dann sieht der Verlauf so aus:
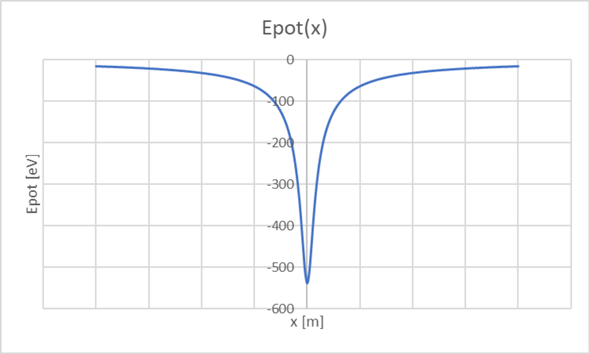
Da Epot bei x=0 negativ ist, muss dort Ekin größer sein als in unendlicher Entfernung. Das bedeutet, die Geschwindigkeit wird von links nach rechts bis x=0 immer größer und dann wieder kleiner. Selbst bei Anfangsgeschwindigkeit Null wird das Elektron durch die beiden Ladungen durchfliegen können.
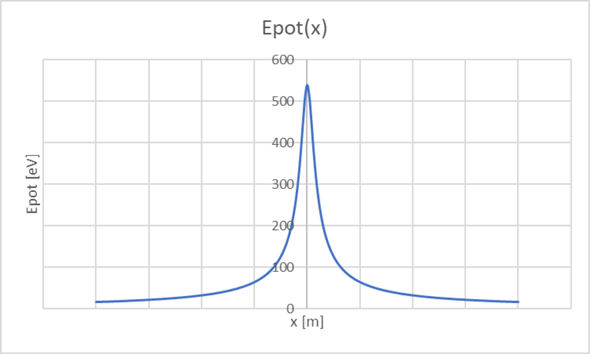
Wenn Q hingegen negativ ist, stoßen die großen Ladungen das Elektron ab. Die Energie sieht dann so aus:
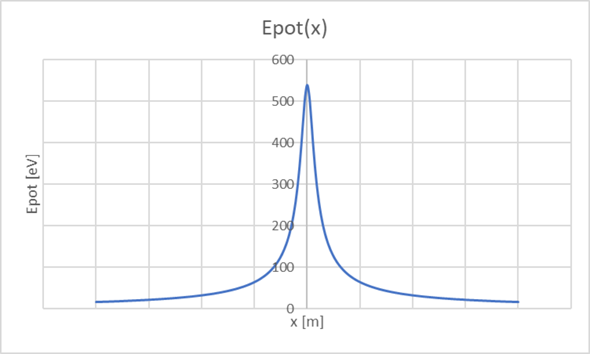
In diesem Fall braucht das Elektron im Unendlichen mindestens eine kinetische Energie von etwa 540eV um den Potenzialwall überwinden zu können. Ansonsten wird es zurückgeworfen.
Ich denke also, dass hier ein Angabefehler vorliegt.
EDIT:
Ich denke nach wie vor nicht, dass die Aufgabe gut durchdacht ist:
Wie definiert sich "durchschießen" ?
Wenn
- das Elektron am anderen Ende für ewig weiterfliegen soll, muss dafür seine Energie ausreichen. Die Gesamtenergie bleibt ja erhalten und ist die Summe aus kinetischer und potenzieller Energie.
- sich das Elektron in die Nähe der Ladungen begibt, wird die potenzielle Energie negativ und die kinetische Energie größer.
- es sich am Ende sehr sehr weit entfernen kann (quasi ewig geradlinig weiterfliegt) ist, bleibt die kinetische Energie am Ende konstant; die Gesamtenergie ist in diesem Fall also E>0.
- die Energie dafür nicht ausreichend ist, also E<0, kann es nicht ewig weiterfliegen und ist quasi eingefangen.
Ich habe hier drei Fälle unter Python simuliert:
- Zwei positive Ladungen befinden sich bei (0, 5) und (0, -5)
- Die Startposition des Elektrons sei (-10, -1).
Ich habe drei Anfangsgeschwindigkeiten gewählt:
- v=1
- v=3
- v=5
Alle Größen sind normiert damit ich nicht die kleinen Einheiten mitschleppen muss.
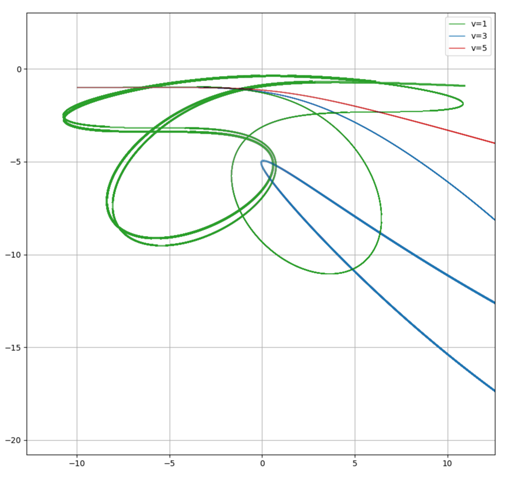
Das Ergebnis sieht sehr chaotisch aus:
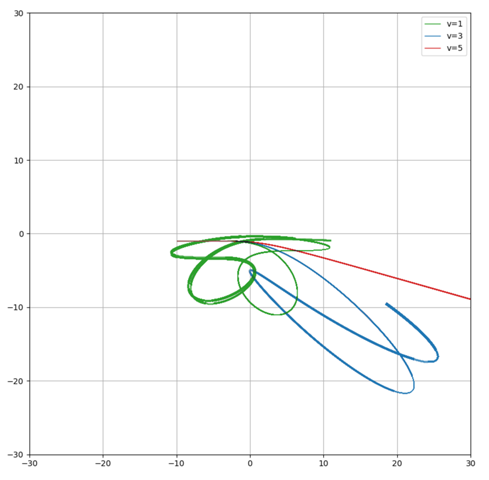
Ausschnitt:
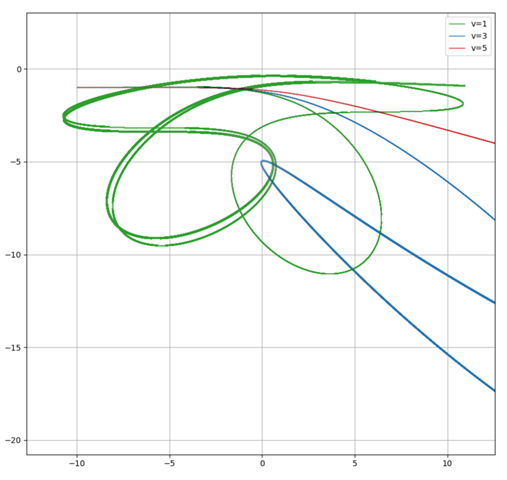
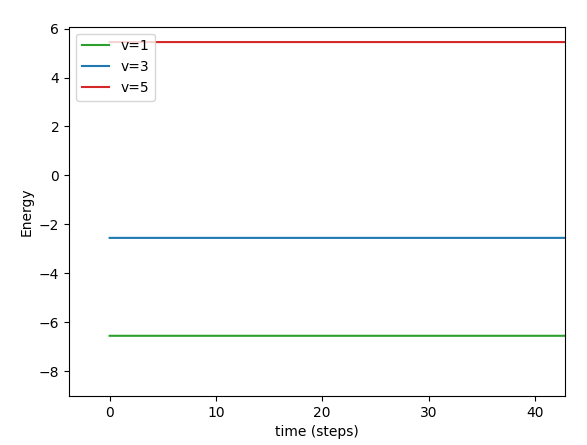
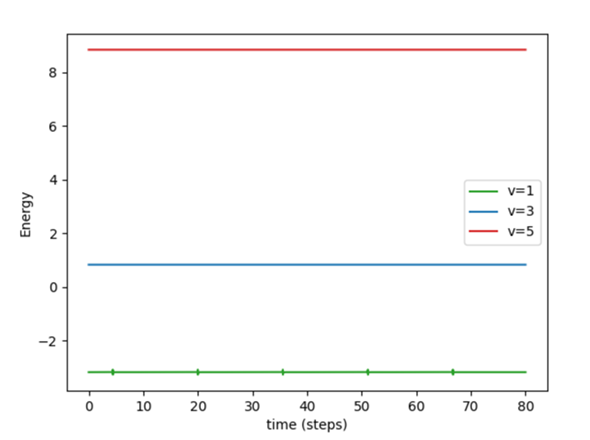
Man sieht, dass hier sehr exzentrische Trajektorien gebildet werden. Vor allem sieht man aber anhand der Energien, dass nur die Kurve mit E>0 (rot) das System verlassen kann:
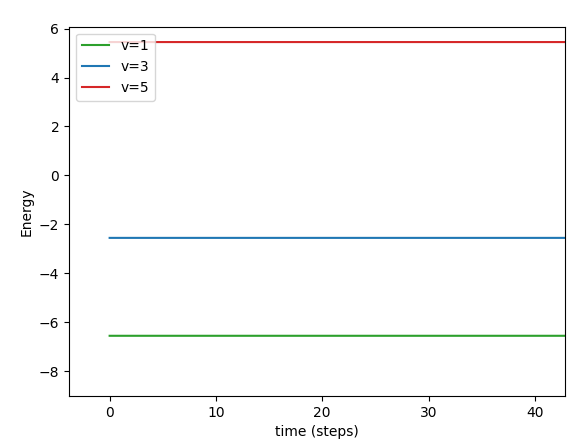
Da die Flugbahnen sehr chaotisch sind, kann man so leicht keine Aussage treffen, was mit dem Elektron passiert.
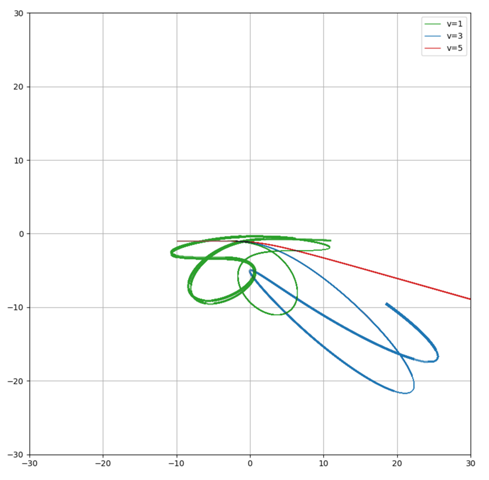
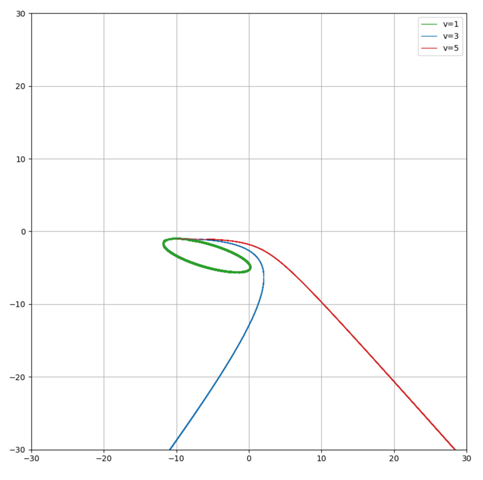
Nehme ich die obere Ladung weg, wird es natürlich das bekannte Kepler-Problem:
Hier ist nur dir grüne Kurve gebunden (elliptische Bahnkurve), da die Energie negativ ist. Die anderen beiden Kurven haben positive Energie und sind daher Hyperbeln.
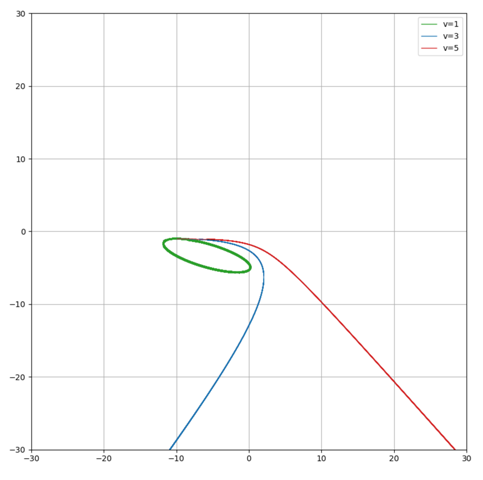
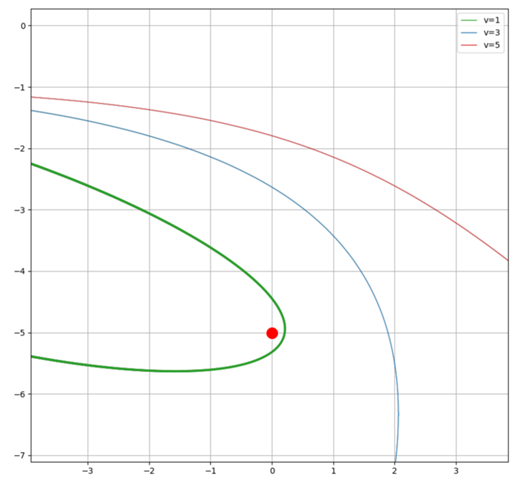
Vergrößert:
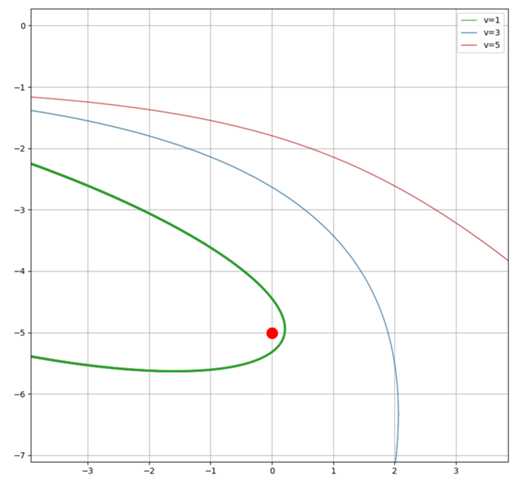
Energie:
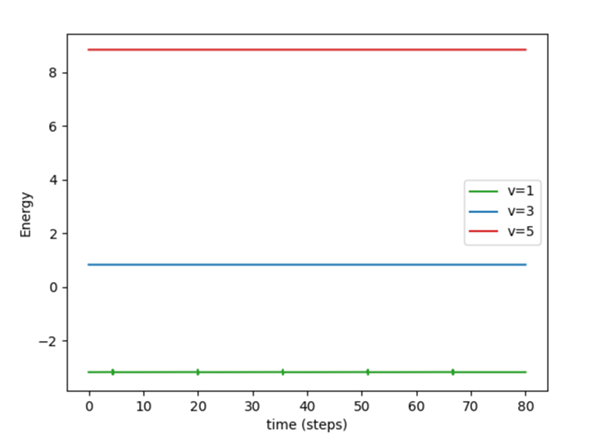
Da die grüne Kurve sehr nahe der Ladung bei (0, -5) zu liegen kommt, ist die Numerik hier etwas ungenau - daher die ganz leichten Abweichungen der Gesamtenergie. Man sieht aber auch hier deutlich das Prinzip - Newton und Kepler lassen grüßen ;-)
Das ist sehr ausführlich. Vielen Dank für deine Zeit. Der Lehrer hat mir den Hinweis gegeben, die Formel ich ich oben gepostet habe zu verwenden. Ich weiß nur nicht genau, wie ich auf rB und ra komme. Könntest du mir beim aufstellen der Formel helfen?
Ich sagte ja schon: es geht um die Gesamtenergie und die muss > 0 sein.
Wie groß ist die Gesamtenergie E? Diese ändert sich ja nicht, ist also eine Erhaltungsgröße: Anfangs, wenn sich das Elektron weit entfernt befindet, habe es den Abstand R:a zur einen und R_b zur anderen Ladung Q.
Die potenzielle Energie ist dort daher
Epot = -1/4π∊_0*1/R_a - 1/4π∊_0*1/R_b
Die kinetische Energie ist anfangs:
Ekin = mv²/2
Und nun muss Eges = EPot+Ekin > 0 sein:
Daraus folgt:
mv²/2 > 1/4π∊_0*(1/Ra +1/Rb)
bzw.
v > wurzel aus (2/4π∊_0m*(1/R_a +1/R_b))
In deine "Formel" gehört die Summe rein, nicht die Differenz - würde ja auch keinen Sinn machen, wenn R_b > R_a wäre, denn dann ist das Argument der Wurzel negativ...
Das sind die Abstände zu den beiden Ladungen zum Zeitpunt des Starts.
Gut...die sind nicht gegeben - was darauf hindeutet, dass die Aufgabe nicht durchdacht ist: Es ist die Rede davon, dass der Startpunkt "unendlich" weit von den Ladungen entfernt liegen soll. Dort ist die potenzielle Energie vernachlässigbar. Damit Eges>0 ist, muss in sehr weiter Entfernung also einfach v>0 sein.
Wenn der Startpunkt nicht im "Unendlichen" liegt, muss man v so groß machen, dass Eges>0 wird - ansonsten bleibt das Elektron gebunden ("eingefangen"). Hier hat man schon ein Epot<0. Die Bedingung dass Eges>0 ist, ist dann die oben angegebene Beziehung.
Ich glaube noch immer, dass es abstoßend zu interpretieren ist, d.h. die beiden Ladungen sollen negativ sein. Dann benötigt man auch im Unendlichen schon eine Mindestgeschwindigkeit.
Aber so macht das Beispiel einfach keinen Sinn. Ich würde dir gerne helfen, aber was nicht geht geht nicht.
Oder es handelt sich num eine Elektron, sondern um ein Positron.
Dein Lehrer kann sich von mir aus hier gerne melden. Dann diskutiere ich das mit ihm.
Ich werde es meinem Lehrer zeigen. Vielen Dank schonmal
Das ist eine Frage aus einem Physik-Buch für das Abitur. Denke da hat sich jemand Gedanken drüber gemacht.
Das ist die Antwort von meinem Lehrer:
Damit das Elektron nicht von einer der beiden positiven Ladungen eingefangen werden kann, muss es eine bestimmte Geschwindigkeit haben, um dem zu entgehen. Der Autor sollte trotzdem die Fragestellung ändern, damit es keine Irritationen gibt.