Mathe Polynomfunktion Fläche?
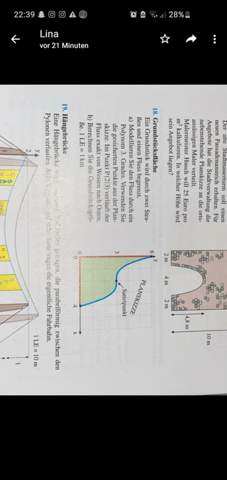
Kann mir wer bei der Nr. 18 a helfen?
3 Antworten
Du hast schon mal drei eindeutige Punkte gegeben. Die beiden Schnittpunkte mit den Achsen und den Sattelpunkt.
Daraus musst du ein Polynom 3. Grades bauen. Das schaut ja irgendwie so aus:
f(x) = a + bx + cx² + dx³ = y
Also musst du die 4 Parameter a,b,c,d finden.
Problem: 3 Punkte, 4 Parameter/Variablen. Das reicht nicht.
Aber bei x=2 ist ja nicht nur y=3, sondern auch ein Sattelpunkt.
Das bedeutet, dass f'(2) = 0 ist. Damit hast du eine vierte Formel, kannst also alles berechnen. Dafür musst du dann halt 1x f ableiten und 2 einsetzen.
Noch mal zur Erinnerung: Für den Punkt (2/3) wäre die Formel:
f(2) = a + b*2 + c* 4 + d * 8 = 3
Und dann halt auflösen.
das ist der Ansatz
f(x) = ax³ + bx² + cx + d
die vier benötigten Bedingungen.
f(0) = 6
f(2) = 3
f(4) = 0
f'(2) = 0
f(x) = ax³ + bx² + cx + d
so einsetzen
3 = 8a + 4b + 2c + d
vier glg , vier unbekannte
Ansatz:
f(x) = ax^3 + bx^2+ cx + d
Schnittpunkte mit den Achsen einsetzen:
f(0) = 6 = 0 + 0 + 0 + d
d = 6
f(4) = 0 = 64a + 16b + 4c + 6
Ableiten für den Sattelpunkt:
f'(x) = 3ax^2 + 2bx + c
f''(x) = 6ax + 2b
Sattelpunkt S(2/3) in f' und f'' einsetzen:
f'(2) = 0 = 12a + 4b + c
f''(2) = 0 = 12a + 2b
Wir haben also ein Glleichungssystem:
64a + 16b + 4c + 6 = 0
12a + 4b + c = 0
12a + 2b = 0
3 Gleichungen, 3 Unbekannte, das lässt sich lösen und es kommt raus:
a = -3/8
b = 9/4
c = -9/2
die Funktion lautet also:
f(x) = -3/8 x^3 + 9/4 x^2 - 9/2 x + 6
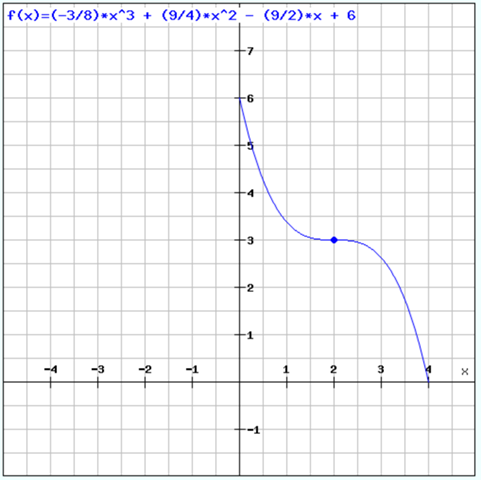
Zur Flächenberechnung müssen wir die Stammfunktion durch Integrieren ermitteln:
F(x) = -3/32 x^4 + 3/4 x^3 - 9/4 x^2 + 6x
Die Fläche A beträgt dann:
A = F(4) - F(0) = F(4) da F(0) = 0
F(4) = -24 + 48 -36 + 24 = 12
A = 12
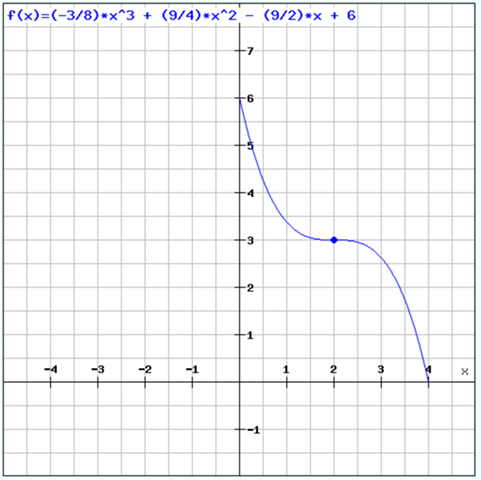
kann man so machen . üblicher ist aber
ax³ + bx² + cx + d