mathe, gymnasium, 9 klasse, zylinder volumenberechnung?
hilfe komme nicht weiter
Aufgabe:
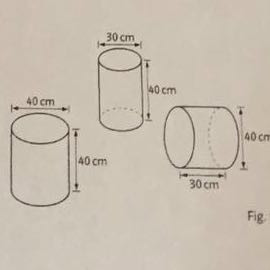
Die linke Tonne ist zu 75% mit Wasser gefüllt.
a) Wie viel Liter Wasser befindet sich in der Tonne?
b) Passt das Wasser in eine der beiden anderen Tonnen?
c) Welche Maße könnte eine Tonne, die 100 Liter fassen soll haben? Gib zwei verschiedene Möglichkeiten
Auf dem Bild sind die jeweiligen Maße zu sehen
3 Antworten
Volumen eines Zylinders V= Grundfläche * Höhe ergibt
V= r^2 *pi *h= d^2 *pi/4 * h
V1=d1^2 * pi/4 * h1=40^2 * pi/4 * 40=50265,48 cm^3 und 1 l=1000 cm^3
also V1= 50,265 l dvon 75% ergibt v1= 50,265 * 0,75=37,699 l
c. V= d^2 * pi /4 * h ergibt h= V *4/(pi * d^2)
wählen wir d= 40 cm und 100 l= 100000 cm^3
ergibt h= 100000 * 4/(pi * 40^2)=79,577 cm
oder wir wählen h= 60 cm ergibt d^2= V * 4/(h*pi)
ergibt d= Wurzel( V *4/(h *pi)= Wurzel(100000 *4/(pi * 60)=46,056 cm
TIPP : Besorge dir privat ein Mathe-Formelbuch aus einen Buchladen,wie den "Kuchling".
Für 30 Euro bekommt man so 600 Seiten mit Formeln und Zeichnungen.
Da brauchst du nur abschreiben..
b. Das ist so einfach,dass brauch ich hier nicht vorrechnen.
Ich will dir jetzt ungern die Hausaufgaben und somit den Lerneffekt vorweg nehmen, aber hier die Ansätze:
1dm³ = 1 Liter
a) Volumenformel für Zylinder anwenden, in dm³ umrechnen, mal 75/100stel nehmen.
b) Die jeweiligen anderen Tonnen in dm³ umrechnen und prüfen ob sie dem Ergebnis aus a) entsprechen
c) Volumenformel gleichsetzen mit 100dm³ und für den Radius einen beliebigen wert einsetzen, dann nach Höhe auflösen. Das gleiche mit einem anderen Radiuswert wiederholen.
Hoffe ich konnte helfen!
Klingt zwar komisch, dass aus 80dm ein Raum aufgespannt wird in den 100Liter reinpassen, aber das liegt daran das eindimensionale maßeinhameiten in dieser Formel 3dimensional gemacht werden, und dementsprechend hoch 3 genommen. (Musst du natürlich nicht für die HA wissen, ist nur die Erklärung warum die Zahlen so merkwürdig klein sind)
Na super was ist das denn !!! :D
Großartiges Phänomen! Aber ich glaube jetzt habe ich es im grossen und ganzen verstanden! Danke für die Hilfe.
Aber dann kommt 1,98943... raus? Wie kann das sein? Wenn ich 100 / (pi • 1^2) rechne kommt 31.83 raus und wenn ich einen höheren Radiuswert nehme, wird die Höhe noch kleiner also auf 1,98943...? Waruuum? :(
Glückwunsch, du entdeckst das Phänomen von Exponentialfunktionen die sich das Menschliche Gehirn leider nicht vorstellen kann! :D
Bei 1² teilst du einen wert insgesamt durch 1 da gilt
1² = 1 und dementsprechend kommt ein hoher wert raus
Wenn du aber
Auf einmal 4² zum Beispiel nimmst TEILST DU DURCH 16, das ist ein sehr hoher unterschied!
Wenn du z.b. nur statt 4 etwas höheres nehmen würdest, z.b 12, dann wäre
12² = 144
Das steigt sehr schnell!!
Deine Ergebnisse sind richtig, aber schwer vorstellbar :D
Jetzt bin ich kurz vorm verzweifeln :( Warum kommt wenn ich beispielsweise 100dm^3 / pi • 4^2 rechne 509,2958... raus? Eigentlich müsste die Höhe doch immer weniger werden desto größer ich den Radius mache oder nicht?
Vorsicht!
Rechne 100dm^3 / (pi * 4^2)
Also das in klammern zuerst, und dann 100 geteilt durch das was du bei pi * 4^2 rausbekommen hast!
Sonst denkt dein Taschenrechner er muss die 100 mal 4² nehmen!!
Super!! Jetzt habe ich es verstanden. Vielen vielen Dank.
Erstmal vielen Dank für diese ausführlichen Erklärungen. Allerdings habe ich noch nicht ganz verstanden, wie genau ich dann nach h auflöse. Also ich habe die Gleichung 100dm^3 = pi • 1^2 • h stehen. Aber wie löse ich dann nach h schlussendlich auf?
100dm³ = pi * 1² * h
Wir teilen die Gleichung mit pi * 1² um nur noch h auf einer Seite stehen zu haben
100dm³ / (pi * 1²) = h
Ich hab jetzt keinen Taschenrechner da aber Kopfrechnen sagt mir so ca
h = 32,5 dm
Wie funktioniert dieses Gleichsetzen, was du in c) benannt hast?
Es gilt die Gleichung
V=Pi*r^2*h
Das tolle an Gleichungen ist, dass du beliebig einsetzen und umformen kannst!
Es müssen 100L rauskommen, also gilt
100dm³ = Pi*r²*h
Jetzt setz für r irgendwas ein was du im Kopf gerade hast! z.B 1
100dm³ = Pi*1²*h
Das löst du nach h auf -> jetzt hast du r und das ausgerechnet h!
Da du aber zwei Möglichkeiten brauchst mach genau das selbe nochmal aber setz für r was anderes ein, z.b. 2!
Das Volumen eines Zylinders berechnet sich mit der Formel:
V=Pi*r^2*h (Pi mal Radius zum Quadrat mal Höhe). Wie du weißt ist Radius der halbe Durchmesser ;) Versuch es mal mit der Formel, solltest so drauf kommen
Eine Sache habe ich noch :D
Wie zum Teufel kann es aber sein, dass der Radius 4 ist und als Ergebnis dann 1,989...dm rauskommt? Wie soll denn in d=8cm und Höhe= 1,989...dm also 19cm 100 Liter Wasser reinpassen?