Mathe Aufgabe Analysis?

Hi, ich bräuchte eine step by step Hilfe wie ich das hier berechnen kann und den Lösungsweg dazu. Wäre euch undendlich dankbar! 👌😫
2 Antworten
Teilaufgabe 1.1. Nullstellen: Die Nullstelle bei x1 =0 hat die Vielfachheit 3 (siehe Exponent von x) und die Nullstelle x2 = 4 ist eine einfache Nullstelle.
Teilaufgabe 1.2 Monotonieverhalten und Extrempunkte
Nullstellen der 1. Ableitung:
Der Extremwert liegt bei x = 3 (Koordinaten HP(3 | f(3)) = HP(3 | 3) und ist ein Hochpunkt (Maximum)
Teilaufgabe 1.3 Wendetangenten
Da bei x=0 ein Sattelpunkt liegt ist die Gleichung der ersten Wendetangente
Der Wendepunkt x1=0 und dessen Tangentengleichung ist oben behandelt. Bleibt noch x2=2 zu betrachten:
Es handelt sich daher um einen Wendepunkt.
Die Gleichung des Wendepunkts lautet:
Teilaufgabe 1.4 Skizze

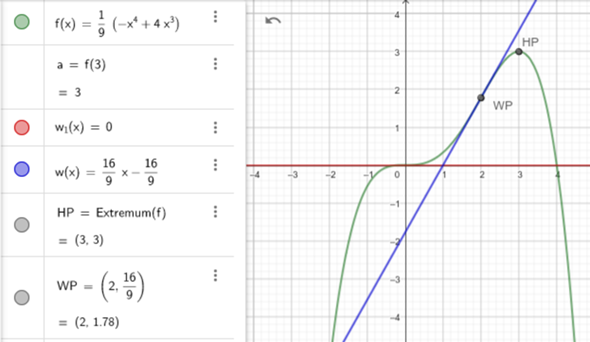
1.1) Funktion faktorisieren
f(x)=1/9*(-x^4+4x^3)=1/9*(x^3(-x+4))
Wann wird die Funktion 0, wenn gilt:
x^3=0 wobei die Vielfachheit der Nulsstelle 3 ist;
und -x+4=0
x=4 einfache Nulsstelle
1.2 erstmal ableiten und die Vorzeichen der Funktion zwischen den Nullstellen ermitteln;
Ableitung und Nullstellen ermitteln:
f'(x)=1/9(-4x^3+12x^2)=1/9(-4x^2(x-3))
f'(x)=0 für
x1/2=0 und x3= 3
Da die erste Nullstelle doppelt ist kann es dort kein VZW geben, deshalb muss man nur links und rechts von 3 schauen;
f'(2)>0
f'(4)<0
Da das VZW bei f'(3) von + auf - wechselt ist f(3) ein Hochpunkt. Im Bereich von (-unendlich;3] ist f streng monoton zuhnemend und im Bereich [3;+unendlich) ist f streng monoton abnehmend
Koordinaten von Hochpunkt:
f(3)=...
1.3) erstmal 2. Ableitung und dann wieder Nullstellen bestimmen und dann mit VZW oder Dritter Ableitung Wendepunkte beweisen;
f''(x)=1/9(-12x^2+24x)=1/9(-12x(x-2))
x1=0 und x2=2
f''(-1)<0
f''(1)>0
f''(3)<0
es gibt also einen VZW bei x=0 und x=2 womit beide Punkte Wendepunkte sind und der Wendepunkt bei x=0 ist auch Sattelpunkt wobei danach in der Aufgabenstellung nicht gefragt wird;
Tangentgleuchung ermitteln, erstmal die Steigung an den Punkten ermitteln:
Erste Ableitung gibt Steigung an:
f'(0)=0
f'(2)=16/9
Jetzt berechnet man die Koordinaten an den Punkten,da die Tangentgleichungen ja die Steigungen der Wendepunkte aufweisen und diese Punke gleich haben;
f(0)=0
f(2)=16/9
Jetzt die Punkte mit der Steigung in die allgemeine Form der Geradengleichung einsetzen und letzten Parameter berechnen;
t(x)=mx+c
t1(0)=0*0+c=0 -> c=0; t1(x)=0
....
t2(2)=16/9*2+c=16/9 ....
1.4)
Mit dem Monotonieverhakten den Extrema, den Wendepunkten und Nullstellen die Funktion im Bereich skizzieren