Mathe Aufgabe?

Hallo Zusammen,

dieser aufgabe ist meine hausaufgabe und ich verstehe sie leider nicht habe schon ein paar erklärungen angeguckt nichts hat jedoch geholfen.

Könnte mir vllt jemand schnell helfen. Vielleicht die erste aufgabe einmal vor rechnen damit ich damit üben kann und somit den rest alleine mache

Dazu muss ich sagen in der aufgabe sollen wir Die Koordinaten berechnen dabei erste ableitung und 0 setzen

Danke im vorraus:)

Answer 1

[verreisterNutzer]

Dazu muss ich sagen in der aufgabe sollen wir Die Koordinaten berechnen dabei erste ableitung und 0 setzen

... dass Du meinst, das dazusagen zu müssen, erklärt komplett, warum Du "ich verstehe sie leider nicht" schreibst.

Wer die Worte "Hoch- und Tiefpunkte" liest und bestimmen soll, kennt sofort das Rezept (das ändert sich in den wesentlichen Teilen bis zum Abi nicht):

• 1. Ableitung berechnen
• 2. Ableitung berechnen
• Nullstellen der 1. Ableitung berechnen
• Für jede gefundene Nullstelle der 1. Ableitung den zugehörigen Wert der 2. Ableitung bestimmen. Ist f''(x) <0, dann ist dort ein Maximum (Hochpunkt) und ist f''(x) > 0 ist an der betreffenden Nullstelle ein Minimum (Tiefpunkt)
• Anschließend bestimmst Du noch den Funktionswert an den gefundenen Nullstellen der 1. Ableitung

Answer 2

[nobytree2]

Einfach zweimal ableiten und erste Ableitung auf Null setzen (Konstanten ohne Anbindung an die Ableitungsvariable fallen in der Ableitung heraus)

$f\left(x\right)'=\left(-x^2-4x^1-1\right)'=2\cdot-x^{2-1}-4\cdot1\cdot x^{1-1}$

$=-2x-4=0\to x=-2$ Das -2 setzen wir in die zweite Ableitung ein

$f\left(x\right)''=\left(-2x-4\right)'=-2$

-2 ist negativ, es gibt also ein Maximum. Das liegt bei (-2 | f(-2)) = (-2 | 3)

Answer 3

[chromakopia]

Genau, du sollst die erste Ableitung berechnen und dann mit 0 gleichsetzen.

Die erste Ableitung berechnet die Steigung der Funktion und wenn diese 0 betraegt ist dort ein lokales Minimum/Extremum.

Beispiel mit der a)

f(x) = -x^2 -4x-1

f`(x) = -2x-4

-2x-4 = 0 | +4

-2x = 4 | / 2

-x = 2 | *-1

x = -2

Diesen Wert setzen wir nun in die zweite Ableitung ein, um herauszufinden, ob es sich um ein Minimum oder Maximum handelt.

f``(x) = -2 --> Wert ist negativ, also ist es ein Maximum.

Um den y Wert herauszufinden, musst du nun -2 in die urspruengliche Gleichung einsetzen.

f(-2) = 3.

Das Maximum liegt also bei P(-2 | 3).

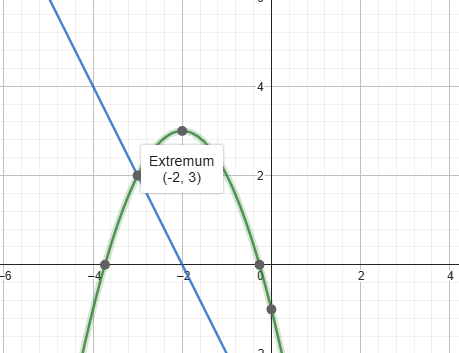
Grafische Darstellung:

Der gruene Graph stellt f(x) dar, waehrend der Blaue die erste Ableitung darstellt. Da kannst du super erkennen, wie die Nullstelle der Ableitung bei -2 liegt.

Comments

[user11111360]

ist bei der b) dann das ergebnis mit der Ableitung 1xhoch2 - 2

?

[chromakopia]

@user11111360

Fast!
1x^2 ist korrekt, weil 3*1/3 = 1 (musst dann nicht die 1 mitschreiben).

-x^2 abgeleitet ist aber nicht 2, sondern -2x. Man nimmt den Exponenten, multipliziert den Koeffizienten damit und zieht dann 1 von dem Exponenten ab.

Bei -x^2 ist 2 der Exponent und auch wenn die Zahl dort nicht steht, aber der Koeffizient von -x ist 1, also steht dort quasi -1x^2.

Dann multipliziert du den Exponenten 2 mit dem Koeffizienten 1 und ziehst von dem Exponenten 1 ab.

Du erhaeltst also -2x^1. Das hoch 1 musst du jedoch nicht mitschreiben, also ist es einfach -2x.

Verstaendlich?

[user11111360]

@chromakopia

also kommt somit für x 2 raus und wenn ich das einsetze damit ich y rauskriege kommen 1/6 also 1,16Periode raus

[chromakopia]

@user11111360

Ich rechne das ganze mal nach:

f(x) = 1/3x^3-x^2

f`(x) = x^2-2x

f``(x) = 2x-2

Nun berechnen wir die Nullstellen der ersten Ableitung:

x^2-2x = 0

Wir sehen, dass wir keine alleinstehende Zahl haben, mit der wir x aufloesen koennen. Deshalb klammern wir x aus:h x*(x-2) = 0

Der Satz vom Nullprodukt sagt, wenn das Produkt zweier Faktoren 0 ist, so ist mindestens einer dieser Faktoren gleich 0.

Hier sind unsere Faktoren x und x-2. Das bedeutet, dass x = 0 und x-2 = 0.

Die erste Nullstelle, x1 = 0, haben wir jetzt schon.

Nun berechnen wir noch die Nullstelle der Klammer.

x-2 = 0 | + 2

x = 2

Die zweite Nullstelle ist also x2 = 2.

Jetzt wollen wir herausfinden, wo es sich um ein Maximum und wo es sich um ein Minimum handelt. Wir fangen mit der ersten Nullstelle an.

f``(0) = -2 -> Es handelt sich um ein Maximum

Jetzt die zweite Nullstelle:

f``(2) = 2 -> Es handelt sich um ein Minimum.

Jetzt musst du beide Werte noch in die urspruengliche Funktion einsetzen:

f(0) = 0 -> Maximum liegt bei P(0 | 0)

f(2) = -1.333 (Periode) -> Minimum liegt bei P(2 | -1.333)

Graphische Darstellung: https://imgur.com/a/dFPLUDX

Hier ist der gruene Graph die urspruengliche Funktion und der blaue Graph die erste Ableitung. Dort kannst du sehen, wie die erste Ableitung nicht nur eine, sondern zwei Nullstellen besitzt, weshalb es auch zwei Extremwerte gibt.

Verstanden?