Mathe Abitur Aufgabe?

Hallo! Die Aufgabe lautet:

Von allen Jugendlichen eines Landes im Alter von 14 bis 25 Jahren sind 49,20% weiblich. 47,10% der Jugendlichen erledigen ihre FInanangelegenheiten regelmäßig mittels Smartphone oder Tablet. Der Antue der Jugendlichen, die weiblich sind und ihre Finanzen regelmäßig mittels Smartphone oder Tablet erledigen beträgt 19,68%.

Bestimmen sie die Wahrscheinlichkeit dafür, dass eine unter den Jugendlichen zufällig ausgewählte Person entweder männlich ist oder ihre Finanzen regelmäßig mittels Smartphone oder Tablet erledigt.

Meine Idee wäre der Additionssatz: P(A)+P(B)- P(A u B)

50,8% + 47,10% - 27.42% = 70,48%

Die wirkliche Lösung lautet jedoch: 19,68% + 23,38% = 43,06%

Wieso kann der Additionssatz nicht angewendet werden, meiner Meinung nach wäre dieser richtig.

Answer 1

[Rammstein53]

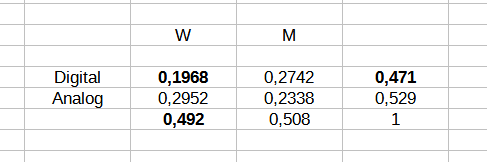
Die Vierfeldtafel sieht so aus:

Ich komme ebenfalls auf Deine Lösung. Die angebliche Lösung von ca. 43% kann schon deshalb nicht stimmen, weil bereits ca. 50% der Jugendlichen männlich sind.

Die angegebene Lösung wäre nur dann korrekt, wenn die ausgewählten männlichen Jugendlichen kein digitales Gerät, die weiblichen dagegen ein digitales Gerät nutzen sollen, also p(M ∩ Analog) + p(W ∩ Digital). Dieses Ausschlusskriterium alternativer Eigenschaften lässt sich aus der Aufgabenstellung jedoch nicht herauslesen.

Lösungsweg 1:

p(M ∪ Digital) = p(M) + p(Digital) - p(M ∩ Digital) = 0.508 + 0.471 - 0.2742 = 0.7048

Lösungsweg 2:

p(M ∪ Digital) = p(M) + (W ∩ Digital) = 0.508 + 0.1968 = 0.7048

Lösungsweg 3:

p(M ∪ Digital) = 1 - p(W ∩ Analog) = 1 - 0.2952 = 0.7048