Logik Rätsel aus Informatik Klausur unlösbar?

ziel ist es, alle Felder auf 1 zu bekommen, nur in dem man eine gesamte Spalte oder Zeile invertiert. Also bei vier zum Beispiel wäre das 1001 oder bei B von oben nach unten 110101.
kann es sein, dass diese Aufgabe nicht lösbar ist?
1 Antwort
Ich glaube ich habe einen Beweis für die Unmöglichkeit dieses Rätsels gefunden, aber ich hoffe jemand anderes kann das überprüfen.
Ich wäre wirklich froh, wenn jemand einen noch einfachereren Weg präsentieren könnte! :)
Ich behaupte zunächst einmal:
Angenommen das Ursprungsproblem wäre lösbar. Dann gäbe es eine Lösung auch für dieses Problem:

Warum ist das so? Naja, das ist einfach zu sehen.
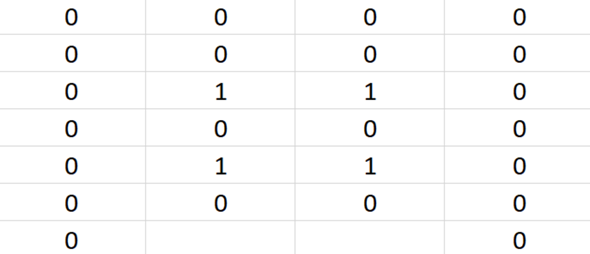
Das Ursprungsproblem:

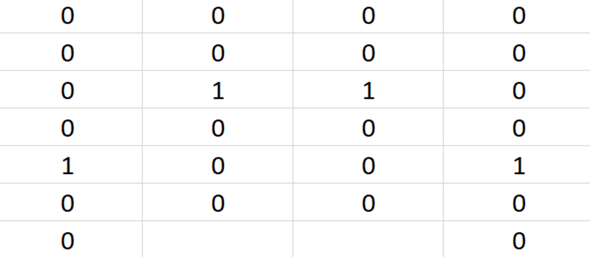
Lässt sich durch invertieren von Zeile 2 umformen zu (1) :

Jetzt betrachten wir nur die Reihen 1 und 2 auf Spalten A und B, schränken uns also ein auf (2):

Wenn es eine Lösung von dem Ursprungsproblem geben würde, dann gibt es also auch eine Lösung von (1) und gibt es davon eine Lösung, gibt es eine Lösung von diesem kleinen Problem (2).
Denn: In einer Lösung von (1) würden wir auf ganz (2) nur Einsen sehen. Außerdem wirkt jeder Schritt der Lösung zu (1) entweder nicht auf (2), oder wenn er auf zwei wirkt, dann durch Invertierung von Zeile 1 oder 2 oder durch Spalte A oder B. Die Wirkung auf (2) einer Lösung von (1) können wir also äquivalent zu einer Lösung von (2) umformen, wenn wir Zeile 1' und 2', beziehungsweise Spalten A' und B' des Systems (2) immer dann invertieren, wenn die jeweilige Zeile/Spalte (ohne ') des Systems (1) invertiert wird.
Wir haben das Problem also deutlich vereinfacht. Wir müssen für die Unmöglichkeit von (1), beziehungsweise dem Ursprungssystem (deren Lösbarkeit ist trivial äquivalent) nur noch die Unlösbarkeit von (2) zeigen.
Fokussieren wir uns also auf (2):

Das dies nicht lösbar ist, ist jetzt die einfache Beobachtung: Starten wir in (2) mit einer ungeraden Zahl von Einsen, so bleibt die Zahl der Einsen ungerade.
Dafür müssen wir nun nur den Fall, dass wir mit einer 1 starten, beobachten. Da der Fall für 3 Einsen äquivalent zum Fall mit einer Null ist. Wenn die Anzahl der Nullen ungerade ist, ist es auch jene der Einsen.
Der Fall für die eine 1 ist nun aber klar, wenn wir die vier Invertierungen einfach ausrechnen. Damit sind wir auch fertig. Wir können (2) nicht lösen, also lässt sich auch (1) und damit auch das Ursprungsproblem nicht lösen.