Kugel auf Feder, wie komme ich auf zusammengedrückte Strecke?
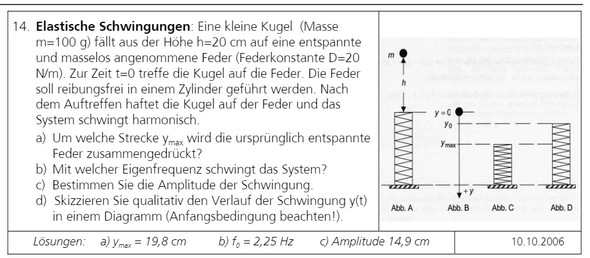
Im Anhang befindet sich die Aufgabe.
Muss ich für y-max die potentielle, kinetische und Spannenergie gleichsetzen?` Wenn ja, dann wie?
1 Antwort
Die Kugel besaß zur Beginn eine Potentielle Energie:
Epot = mgh(0)
Bei einem Abstand von ds zur entspannten ruhenden Feder folgt eine Energiedifferenz von:
dE = ds*m*g
Diese wird beim Fall in kinetische Energie umgewandelt. Die Kugel trifft nun auf die Feder und es kommt aufgrund des Impulses der Kugel zu einer Kontraktion der Feder. Die Federkraft in Abhängigkeit der Länge dx, der Längenänderung der Feder, folgt zu:
F = D*dx mit Federkonstante D
Die Arbeit die dabei verrichtet wird ist gegeben durch:
dW = 0.5*D*dx² , sie entspricht der potentiellen Energie die in der Federposition gespeichert ist. Wir suchen nun den Punkt indem die kinetische Energie zu Null wird:
--> dE + m*g*dx = dW = 0.5*D*dx²
Wir fragen uns nun um welche Strecke die Feder zusammengedrückt wird, wir stellen also nach dx um:
--> 0 = dx² - 2*m*g*dx/D - 2*dE/D
Eine quadratische Gleichung deren Lösung mittels pq-Formel bestimmt werden kann.Wir erhalten:
dx(1|2) = mg/D +/- sqr((m²g²/D²) + 2*dE/D)
und da ein negatives Ergebnis keinen Sinn macht, folgt:
dx_max = -mg/D + sqr( (mg/D)² + 2dE/D )
Einsetzen der gegebenen Werte in unsere Gleichung liefert uns dann:
m = 0.1kg , h = 0.2m , g = 10m/s² , D = 20N/m
dx_max = 0.2m , wobei dies in guter Näherung 0.198 m entspricht.
Die DGL die ein solches ideales und reibungsfreies System beschreibt lautet hier in diesem Fall:
Fges = Fg - F_Feder
--> m d²x/dt² = m*g - D*dx
Wir folgern daraus:
d²x/dt² + (D/m)dx = g
Die Eigenfrequenz erhalten wir dann über die Lösung der homogenen DGL:
d²x/dt² + (D/m)dx = 0
Die charakteristische Gleichung folgt zu:
k² + (D/m) = 0 --> k² = - (D/m)
--> k(1|2) = +/- i *sqr( D/m )
Wir erhalten damit also als Eigenfrequenz f0:
sqr(D/m)/(2*pi) = f0 = 2.25 Hz , auch dies stimmt mit der Lösung überein.
Für den Rest bin ich zu faul ...