Krümmung von Graphen - schneiden sich die Graphen?
Folgende Frage: Zwei Funktionen f und g seien auf ganz ℝ definiert und hinreichend oft differenzierbar. Der Graph von f sei überall linksgekrümmt, der Graph von g überall rechtsgekrümmt. Ferner gelte f(0) < g(0). Warum schneiden die Graphen sich notwendig?
Danke für jede Hilfe!
1 Antwort
Servus,
Ein Graph ist dann links gekrümmt wenn das a>0 ist. Ist a<0 ist der graph der Funktion rechts gekrümmt.
Also Bsp:
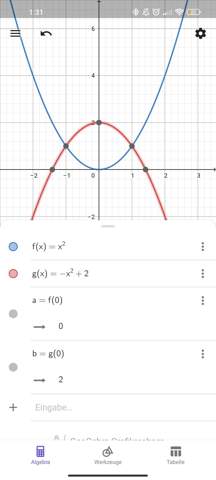
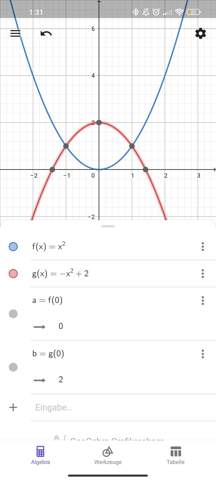
f(x) =1x^2 - - > das a ist 1 also größer Null.= links gekrümmt. Beweis siehe Bild.
g(x) =-1x^2 - - > das a ist - 1 also kleiner Null. =rechts gekrümmt.
Wenn nun auch noch der Graph g im selben Punkt über dem Graphen f liegt (also im Koordinatensystem) f(0)<g(0) dann schneiden sich die Graphen siehe Bild. Hier ist beispielsweise eine Verschiebung mit d=+2 für g.
Ich hoffe man versteht was ich meine bei Fragen melden. Lg