Kann mir jemand bei dieser Mathe Aufgabe helfen?
In einer Turnhalle hängt ein Kletterseil so, dass noch 50 cm dieses Seils auf dem Boden liegen. Zieht man das untere Seilende 2,5 m zur Seite berührt es gerade noch den Boden. Wie lang ist das Seil?
Ich denke mal das hat mit dem Satz des Pythagoras zutun, denn beim Ziehen nach rechts bildet sich ja sozusagen ein Dreick.
Würde mich über Hilfe echt freuen, danke.
5 Antworten
Ja, es bildet sich ein Dreieck. Mache eine Planskizze und trage dort bekannte und unbekannte Größen ein. Nenne die Länge des Seiles "x", dann ist eine Kathete x - 50cm lang, die andere 250cm, die Hypothenuse ist x cm lang. Nun eine quadratische Gleichung für x aufstellen und x ausrechnen.
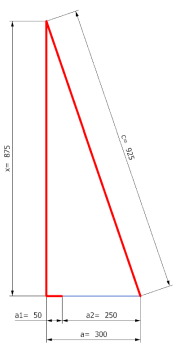
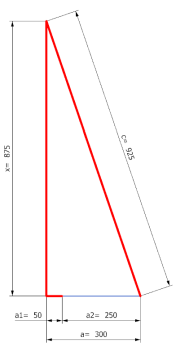
x = Höhe der Turnhalle
c = Seillänge (x + a1)
(x + a1)² - x² = a²
(x + 50)² - x² = 300²
(x² + 100x + 2500) - x² = 300²
100x + 2500 = 300²
100x + 2500 = 90000
100x + 2500 = 90000 | :100
x + 25 = 900
x = 875 cm
Höhe der Turnhalle ist 875cm (8,75m).
Länge des Seils:
c = x + a1
c = 875 + 50
c = 925cm (9,25m)
Ja.
Du kennst a= 2,5 m.
und du weißt, dass b = c -0,5
Also einfach die Werte einsetzen und rechnen.
Pythagoras.
Mache dir doch eine Skizze.
Das rechtwinklige Dreieck besteht aus der Hypotenuse (Seite "c", die gesuchte Länge des Seils), der Seite "b" = 2,5m und der Seite "a" (Länge des Seils minus 0,5 m).
Die Formel lautet also:
c^2 = 2,5^2 + (c - 0,5)^2
Nach "c" umstellen und ausrechnen. Es müssten 6,5 m (Länge des Seils) rauskommen.
Das solltest du allein können!
Was bedeuten würde du musst die Höhe vom Dreieck berechnen, wenn du weißt das eine seite 2,5 m hätte kannste die anderr Seite mit genauso 2,5 metern berechnen errechnest daraus die lange seite und dadurch die Höhe die ziehst du ab von den 50m
Dann haste nen Ergebnis.