Kann Excel die Fibonacci-Folge weiter führen?
Hallo an alle die mit Excel arbeiten,
weiß jemand ob Excel anhand einer vorgegebenen Zahlenfolge die nächste logische Zahl herausfinden kann?
Meist tippt man 1,2,3 ein und zieht das runter und es kommt 4,5,6,... also das was man erwartet.
Aber wie ist es mit anderen Reihenfolgen, kann Excel auch die weiterführen? Hab beispielsweise die Fibonacci Folge ausprobiert
1,1,2,3,5,8,13,21, ... danach kommt die 34 Excel spuckt mir die 28 aus
Auch mit mehr Zahlen ist die Vorhersage eher mau. Kennt sich da jemand besser aus ?
Grüße
7 Antworten
Zunächst ist EXCEL frei programmierbar, d.h. der User davor hat alle Möglichkeiten...
Was Du vermutlich meinst, ist die Auto-Vervollständigung.
Da jedoch keine Randbedingungen angegeben sind, gibt es unendlich viele Algorithmen, um die Zahlenfolge 1,1,2,3,5,8,13,21,...
fortzuführen:
- Regression,
- Polynomanalyse:
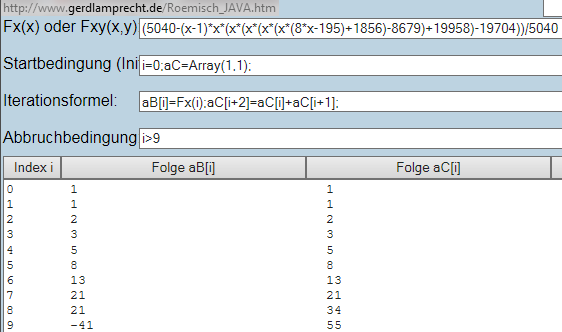
(5040-(x-1)*x*(x*(x*(x*(x*(8*x-195)+1856)-8679)+19958)-19704))/5040
siehe Bild im Anhang per Iterationsrechner
http://www.gerdlamprecht.de/Roemisch_JAVA.htm
- Rekursion
- Nachkommastellen irrationaler Zahlen wie Pi
- kann Tage lang so weitermachen, da ich über 300 Funktionen kenne...
Woher soll EXCEL oder wir hier DEINE Gedanken kennen?
Normale Einstellungstests wollen meist nur primitive Folgen, die in der Schule bereits durchgenommen wurden!
Natürlich ist die Fibonacci(x) bekannter als
f2(x)=(5040-(x-1)*x*(x*(x*(x*(x*(8*x-195)+1856)-8679)+19958)-19704))/5040
aber nicht unbedingt "einfacher":
Wenn man Fibonacci(10^9) und f2(10^9) exakt berechnen soll, ist f2 sehr viel einfacher und schneller!
Außerdem sind wir heute schon weiter und kennen neben der rekursiven auch die explizite Formel:
Fibonacci(x)=([(1 + sqrt(5))/2]^x - cos(Pi*x)/[(1 + sqrt(5))/2]^x)/sqrt(5)
Bei der Suche nach Zahlenfolgen hilft
https://oeis.org/search?q=1%2C1%2C2%2C3%2C5%2C8%2C13%2C21&language=english&go=Search
und antwortet mit 9 Seiten voller bekannter Folgen!
Natürlich wird in einem Einstellungstest für Polizisten nicht nach Nachkommastellen-Algorithmen oder
Polynomen größer Grad 3 gefragt.
Eine Software, die Deinen Wünschen nahe kommt, ist
http://www.wolframalpha.com/input/?i=1,1,2,3,5,8,13,21,...
da eine Wissensdatenbank dahinter steckt.
Ich analysiere Folgen oft hier:
http://www.gerdlamprecht.de/Mittelwerte.html
man sieht sofort Differenzen und Faktoren zwischen den Gliedern
und am Ende der Seite bekommt man das Interpolationspolynom zur Folge.
In der Experimentalphysik verwendet man jedoch Regressions-Software,
da man die physikalischen Gesetze dahinter sucht:
f3(x)=round(0.7201302406*exp(0.4819215625*x)+0.2798697035*exp(-27.46567378*x))
{kommt der exakten Formel schon sehr nahe, berücksichtigt jedoch nicht den cos-Anteil}
und ist ab f3(12)=234 etwas zu groß.
P.S.: Wenn ich Einstellungstests erstellen sollte, würde die Frage beginnen mit: "Finde zu der gegebenen Zahlenfolge je mindestens 4 Algorithmen, die anders fortgesetzt werden..."
Oder es würden Randbedingungen gegeben sein (z.B. keine Nachkommastellen-Algorithmen, keine Polynome, ...)
Erst dann weiß ich, ob der Bewerber intelligent ist, oder nur das behalten hat, was ein Lehrer mal vorsagte...
zu: "... rekursive Vorschrift herausfinden..."
gegeben: Folge 2,3,5,7,11
rekursive Formel:
aD[i+1]=aD[i]+1+i*5/2-pow(i,2)*2+pow(i,3)*1/2;
ergibt: 2,3,5,7,11,22,48,100
ABER Einstellungstest sagt FALSCH,
gesucht waren die Primzahlen!!!
Verstehst Du nun, was ich meine?
Ich bin über das "Excel" Stichwort zu dieser Frage gekommen. Ich ziehe an der Stelle mal kurz meinen Hut vor den mathematischen Aspekten, die Du hier erläuterst. Irgendwie faszinierend, selbst wenn "Interpolationspolynome" eher Schockgefühle in mir auslösen.
unter http://www.gerdlamprecht.de/Zahlenfolgen.html
habe ich zu fast jeder Folge immer 3 unterschiedliche Algorithmen, die man mit 1 Klick online per Iterationsrechner nachrechnen kann.
Bei der Folge 5,5,4,7,9,5
habe ich über 23 Algorithmen...
aber keiner konnte mir sagen, an was der Aufgabensteller bei testedich.de gedacht hatte...
,
Excel kann das nicht können.
Was man machen kann, ist eine Suche in http://oeis.org
Gibst du 1,2,3,5 rein, kommt Fibonacci raus, aber auch viele andere Möglichkeiten, diese Zahlenfolge fortzuführen.
http://oeis.org/search?q=1%2C2%2C3%2C5%2C&language=english&go=Search
Excel scheint so was wie eine lineare Regression durchzuführen. Arithmetische Folgen kann Excel also weiter führen. Warum es mit geometrischen und ähnlichen Folgen nicht geht, liegt wohl daran, dass dann die Kunden fragen würden, warum nicht auch jene andere Art von Folge automatisch fortgesetzt wird usw. - es gibt ja unendlich viele Möglichkeiten, Folgen zu erstellen.
Ja wie du hier sehen kannst, ist Excel schlau genug: http://www.excel-easy.com/examples/fibonacci-sequence.html
Die Fibonacci-Folge ist natürlich nur ein Beispiel. Aber meistens muss man bei Excel bissel rumprobieren bis die Software versteht was du willst. Aber wenn es eine mathematische Logik gibt, sollte es grundsätzlich kein Problem sein.
auch hier gebe ich die Folge direkt vor,
mich interessiert eher ob das Ding diese Folge ohne Kenntnis der Vorschrift selber weiter führen könnte.
Excel löst nicht von sich aus irgendwelche Rätsel oder analysiert Zahlenfolgen. Es ist in erster Linie immer noch eine Tabellenkalkulation und auf klaren Input angewiesen.
Keiner kennt die Gedanken eines anderen. Meine eigenen werden auch erst klarer wenn ich die Meinung anderer dazu einhole.
Wahrscheinlich sollte meine Frage eher lauten
" Kann man mit excel aus einer Zahlenfolge die rekursive Vorschrift herausfinden, ohne diese selbst zu kennen ? ( beispielsweise gibt man die Fibonacci Folge vor, und das Ding erkennt das es genau diese mathematische Folge ist.)"
Bei Einstellungstests wird diese Aufgabe gerne gestellt und Menschen können diese (ab und zu ) auch lösen. Interessant ist welche Software das auch hinbekommt. Vermutlich benötigt man dafür sowas wie Maschine Learning.
trotzdem Danke