IQ Test Zahlenreihe 1,1,2,3,5?
Man musste die Zahlenreihe logisch weiterführen. Leider konnte man die Lösungen der einzelnen Aufgaben im Nachhinein nicht sehen.. Meine Lösung war 6 da ich mir dachte: 1+1 =2, 2+3 = 5, 5+6=11 usw.. Also immer die darauffolgende Zahl addieren. Stimmt das?
9 Antworten
Es würde mit acht weiter gehen soll weit wie ich das sehe ist das die fibonacci Folge also addiert du so 0+1=1 1+1=2 1+2=3 2+3=5 5+3=8 usw
das ist die fibonacci-folge
zahl 3 entsteht aus der summe von zahl 1 + zahl 2
also:
1 + 0 = 1
11
1+1=2
112
1+2=3
1123
2+3=5
11235
5+3=8
112358
und so geht es immer weiter
1,1,2,3,5,8,13,21,34...
Natürlich kann man die Folge auch mit 6 weiterführen -> eine mögliche Funktion dazu lautet:
(24-(x-1)*x*(x*((x-11)*x+40)-56))/24
Da das aber zu kompliziert ist und die IQ-Ersteller selbst nicht so intelligent sind und Randbedingungen weglassen, wird einfach immer nur abgeschrieben...
Außer Fibonacci-Folge und Primzahlen werden immer nur die 4 Grundrechenarten gefragt ... manchmal auch abwechselnd (wechselnde Grundrechenarten kommen in der Natur so gut wie nie vor!).
Es gibt über 300 Funktionen -> aber nur 4 +2 werden in Tests abgefragt.
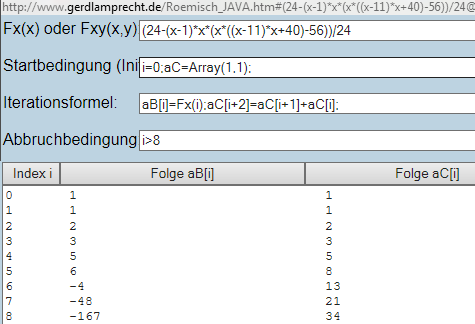
Der Iterationsrechner zeigt 2 mögliche Folgen nebeneinander
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#(24-(x-1)*x*(x*((x-11)*x+40)-56))/24@Ni=0;aC=Array(1,1);@N@Bi]=Fx(i);@Ci+2]=@Ci+1]+@Ci];@Ni%3E8@N0@N0@N#
(Link endet mit N# )
Die rekursive Schreibweise für die einfache Fibonacci-Folge lautet:
aC[i+2]=aC[i+1]+aC[i]; mit Worten: das neue Feld-Element ist die Summe aus den beiden Vorgänger-Elementen.
(also das 3. Element ist Summe aus Element 1 und Element 2)
Statt Element kann man auch Feldvariable oder Array-Element sagen.
Du hast bis 2+3=5 auch richtig verstanden, ABER dann statt die Feld-Elemente aC[3] = 3 und aC[4]=5, also
3 + 5 = 8 = aC[5]
hast Du die Index-Elemente (also das Innere der Eckigen Klammern entspricht im Bild die erste Spalte Index i ) genommen.
Am Anfang hast Du ja auch nicht 0 + 1 , sondern 1+1 gerechnet!
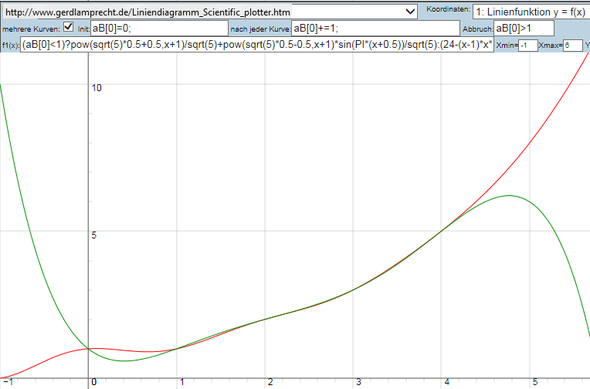
Wenn man beide Funktionen mit expliziten Funktionen Zeichnet:
http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
mi
(aB[0]<1)?pow(sqrt(5)*0.5+0.5,x+1)/sqrt(5)+pow(sqrt(5)*0.5-0.5,x+1)*sin(PI*(x+0.5))/sqrt(5):(24-(x-1)*x*(x*((x-11)*x+40)-56))/24
sieht man die Übereinstimmung der 5 vorgegebenen Punkte
Bild 2
1+1 =2, 2+3 = 5, 5+6=11 Wenn das die Aufgaben waren und man soll die nächste Zahl sagen ist es 12. Es ist das vorherige Ergebnis plus 1. 1+1=2. 2+(2+1)=5. 5+(5+1)=11. 11+(11+1)=23
Die Fibonacci-Folge, jede Zahl ist die Summe der beiden vorherigen.