Intervallschachtelung Mathe?

Was ist die intervallschachtelung für Wurzel 20 ? :)

LG Chiara

Answer 1

[Willibergi]

Hier einmal bis auf 3 Nachkommastellen:

√16 < √20 < √25
4 < √20 < 5
4,5^2 = 20,25
4 < √20 < 4,5
4,25^2 = 18,0625
4,25 < √20 < 4,5
4,4^2 = 19,36
4,4 < √20 < 4,5
4,45^2 = 19,8025
4,45 < √20 < 4,5
4,475^2 = 20,025625
4,45 < √20 < 4,475
4,47^2 = 19,9809
4,47 < √20 < 4,475
4,473^2 = 20,007729
4,47 < √20 < 4,473
4,472^2 = 19,998784
4,472 < √20 < 4,473
4,4725^2 = 20,0032562
4,472 < √20 < 4,4725
4,4721^2 = 19,9996784
4,4721 < √20 < 4,4725

Und schon haben wir drei Nachkommastellen.

Zum Nachprüfen:

√20 = ca. 4,472135954999580

Ich hoffe, ich konnte dir helfen; wenn du noch Fragen hast, kommentiere einfach.

LG Willibergi

Answer 2

[hypergerd]

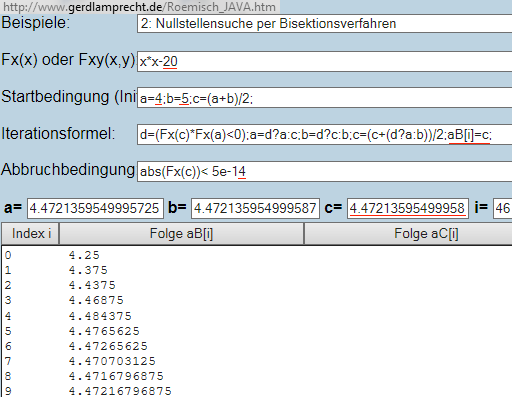
Den Algorithmus (Rechenvorschrift) und die Zwischenergebnisse zeigt der universelle Iterationsrechner im Beispiel 2:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#ZZZZZ0002

Man muss nur die Parameter anpassen (im Bild rot unterstrichen):

Fx(x): statt -2 natürlich die -20

Init: Suchgrenze liegt natürlich zwischen 4 und 5

Iteration: aB[i]=c; um die Zwischenergebnisse tabellarisch aufzulisten

Abbruch: schon bei 5e-14 , da kleinere Fehlergrenzen die Gefahr der Endlosschleife mit sich bringen (double hat nur 15 richtige Stellen)

siehe auch https://de.wikipedia.org/wiki/Bisektion

Bisektion (46 Schritte) ist gegenüber Newton-Iteration (Beispiel 15 mit

a=20;d=2;b=4; -> um die 5 Schritte) sehr viel langsamer bei gleicher Genauigkeit! 

Comments

[questionhny]

Wow danke !! <3

Answer 3

[quentlo]

Am Beispiel von Wurzel 7:
2^2 = 4
3^2 = 9
--> Wurzel 7 liegt irgendwo im Intervall
zwischen 4 und 9 {4;9}
Und so führst du das fort:
2,6^2 = 6,76
2,7^2 = 7,29
--> 2,6^2 < Wurzel 7 < 2,7^2
Nun führst du das solange fort, bis das Intervall so klein ist, dass du einen annehmbaren Näherungswert hast.

Comments

[quentlo]

Ja ja, das ist auch schon sehr lange her, als ich das das letzte Mal gehört habe

[Willibergi]

"Wurzel 7 liegt irgendwo im Intervall 
zwischen 4 und 9 {4;9}"

Intervalle werden in eckigen Klammern angegeben, außerdem sind 4 und 9 exklusiv:

√7 ∈ ]4; 9[

LG Willibergi

Answer 4

[Carmiel]

Bin mir nicht ganz sicher aber ich glaub Wurzel x und 20 aber keine Garantie ob dass überhaupt dass ist nach was du suchst