Integral von exp(x) im Intervall 0 und minus Unendlich
Hallo, ich habe mal gehört, dass die Fläche unterm Graphen genau Pie ist. Aber eine Herleitung wäre ganz gut angebracht.
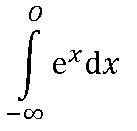
3 Antworten
Zum Formalen:
Auch wenn jeder (ich inklusive) bei berechnungen
integral von - unendlich bis 0(f(x) )=f(0)-f(-unendlich)
hinschreibt, istformal falsch.
Richtig geschrieben muss es lauten:
integral von -unendl.bis 0(f(x))=
=lim k->unendlich (integral von -k bis 0 von (f(x))
=lim k->unendlich( F(0)-F(-k))
wobei F(x) die stammfunktion von f(x) ist
Und ja, da gehört überall nch ein dx hinter inie integralklammer.
In deinem fall ist eben f(x)=e^x
F(x)=e^x+C
F(0)-F(-k)=e^0-e^(-k)=1-1/e^k
wenn nun k gegen unendlich geht, wird e^k ebenso unendlich und damit 1/e^k geht gegen 0.
Damit ist der grenzwert 1-0=1.
Pi sehe ich da zurzeit nirgends :-)
hattest du schon das thema integralrechnung? dein integral hat den grenzwert 1. das integral einer funktion in den grenzen a und b (bei dir also -unendlich und 0) ist die fläche zwischen dem graphen der funktion, der x-achse und den beiden grenzen als senkrechte geraden. das integral berechnest du dabei mit der stammfunktion, was an sich auch logisch ist, aber das dauert lange, es zu erklären und ich will deinem lehrer nichts vorwegnehmen. die stammfunktion ist sozusagen das gegenteil der ableitung, also eine aufleitung, die, wenn man sie ableitet, wieder die ausgangs-funktion ergibt. die stammfunktion von e^x ist die funktion selbst, also e^x. die e-funktion ist die einzige funktion mit dieser eigenschaft.
für die berechnung eines integral musst du die obere grenze in die stammfunktion einsetzen, den wert davon berechnen und dann den wert der stammfunktion für die obere grenze abziehen: e^0 - e^(-unendlich)
da du hier den grenzwert ausrechnest für das integral, musst du jetzt gucken was mit den teilen dieser rechnung passiert: e^0 = 1 e^(-unendlich) = 1:(e^(unendlich)), geht also gegen null.
daraus folgt letztendlich: e^0 - e^(-unendlich) geht gegen 1
dein integral hat also den grenzwert 1.
wie war das? obere grenze minus untere grenze -- also exp(0) - exp(-oo) (grenzwert fpr exp(x) für x gegen -oo = 0), also ist die fläche 1