Hilfeee Mathe: Parabel ist symetrisch zur Geraden
Also ich hab hier eine echt komische Matheaufgabe und kapier sie leider überhaupt nicht... Vieleicht könnte jemand die erklären weil das ist echt wichtig...
Die Parabel p ist symmetrisch zur Geraden g und verläuft jeweils durch den angegebenen Punkt. Ermittle die Gleichung der Parabel p.
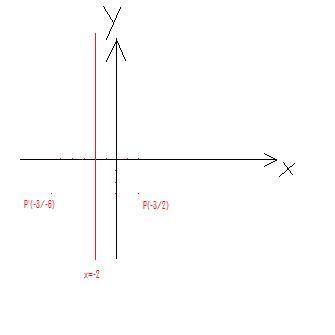
g mit x= -2; P (-3/2); unten offene Normalparabel
lg und schon mal danke Laura
2 Antworten
Eine Parabel hat als Normalfunktion f(x)=ax²+bx+c Wenn diese Symmetrisch zur Geraden g (x=-2) und durch den Punkt P (-3/2) verlaufen soll, kann man die Gleichung lösen, indem man 2 Bedingungen hat: I. 2 = 9a-3b+c II. Symmetrie zu x=-2 Dadurch hast du einen neuen Punkt: P(-3/-6) -3 = 36a-6b+c
Jetzt kannst du die Variabeln ausrechnen (Addition/Substraktion von Gleichungen/Gauss-Verfahren...) und hast die Gleichung der Parabel.
Ich habe gerade genau die gleiche Aufgabe vor mir liegen und frage mich zwei Dinge in bezug auf deine Ausführung:
Hat eine nach unten geöffnete NORMALparabel überhaupt ein a? Meines erachtens ist die Normalparabel ja nur durch x² definiert... und nach unten würde dies -x² bedeuten...
hast du bei deiner zweiten aufgestellten Gleichung die Koordinaten nicht verkehrt herum eingesetzt? Bei : P: y=ax²+bx+c hättest du dann nach dem einsetzten, doch
-6=(-3)²a+b(-3)+c
=> -6=9a-3b+c
Ich kann mich aber auch irren...
y = ax^2 +bx +c
S auf g:
y =c = 4a^-2b +c
mit P (-3/2):
2 = 9a^2 -6b
Parabel p ist symmetrisch zur Geraden g
Dann liegt (-1/ 2) auf p:
2= a^2 -b
LGS lösen.