Hilfe bei der Aufgabenstellung mathe Pyramide?
Die quadratische Grundfläche einer 5m hohen Pyramide hat die Kantenlänge 6cm. Die Spitze liegt Senkrecht über der Mitte der Kante AD
a) zeichne Das schrägbild
b) Bestimme den Neigungswinkel der Seitenfläche BCS gegenüber der Grundfläche
Könnt ihr mir sagen wie man das machen soll?
Also ich versteh nicht wo genau jetzt die Spitze liegen soll? Senkrecht über der Mitte der kannte AD ? Was bedeutet das und die Seite BCS ist was?
2 Antworten
Mach dir eine Skizze, dann kannst du dir die Pyramide besser vorstellen.
Die Pyramide hat ein Quadrat mit den Ecken A, B, C, D. Ihre Spitze heisst S (wie S-pitze).
Die Spitze der Pyarmide liegt gerade (senkrecht) oberhalb der Mitte von AD - also über einer der Quadrat-Seiten, genau über deren Mitte.
Die Seitenfläche B-C-S ist die Fläche zwischen der Quadratseite B-C und der Spitze S.
Zunächst: Ich vermute du hast hier m und cm vermischt, richtig?
Ich gehe jetzt mal davon aus, dass alles in cm ist.
Ich habe das jetzt mal aufgezeichnet wie die Pyramide aussieht.
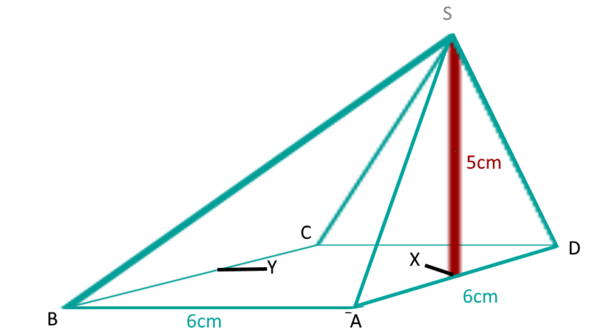
Du siehst also, dass BCS eine Fläche ist. Und gefragt ist ja der Winkel, in dem diese Fläche zur Grundfläche ABCD liegt.
Hierzu nimmt man ein Dreieck an zwischen den Punkten S, Y und X. Man kennt die Länge der Strecke SX (5cm). Die Länge der Strecke XY kennt man ebenfalls (6cm).
Ich denke den Rest solltest du alleine hinbekommen, oder?
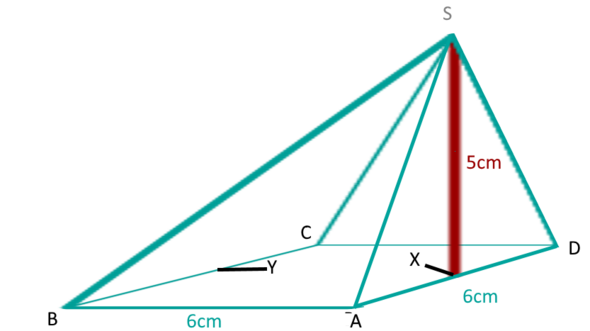
Danke! Also musste man dann eigentlich nur noch:
tan x = 5/6 = 0,83
tan^-1 (0,83) und dann hat man den Winkel oder wie?