Wie kann man bei der Knickpyramide das Volumen berechnen?
Hey,
ich komme bei einer Matheaufgabe nicht weiter und würde mich sehr über Hilfe freuen!!
Aufgabe: Bei der Knickpyramide des Snofru wird auf einem Quadrat mit 189m Seitenlänge zunächst bis auf eine Höhr von 49 m mit einem Neigungswinkel von 54 Grad gebaut. Von dort wird mit einem Neigungswinkel von 43 Grad bis zur Spitze in ursprünglich 104 m Höhe weiter gebaut. Nimm an, dass die Pyramide vollständig aus Stein besteht und berechne das Volumen der insgesamt verbauten Steine.
Hinweis: Die Neigungswinkel ist der Winkel, der von den Seitenflächen mit der Grundfläche eingeschlossen wird. Nutze die Trigonometrie in einem rechtwinkligen Dreieck.
1 Antwort
Es liegt vor : eine Py auf einem Py-Stumpf
....
...
..
.
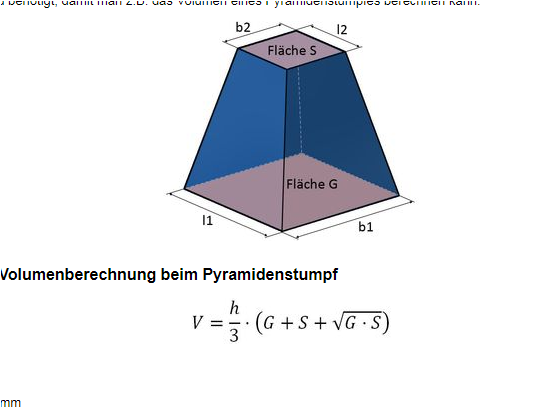
für das Vol eines Py-Stumpfes gibt es eine Formel . Diese selbst zu entwickeln ( siehe wiki ) wäre Wahnsinn.
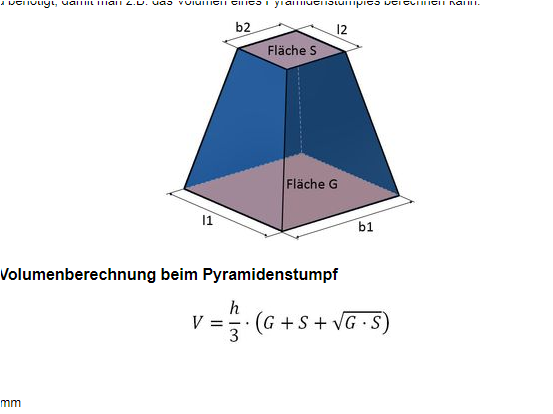
Aber man braucht die Kantenlängen der oberen Fläche .
.
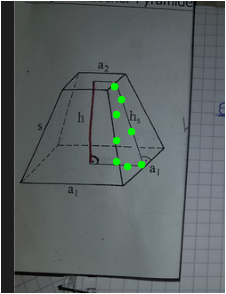
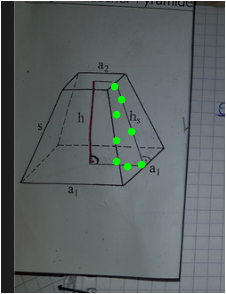
Dazu diese Zeichnung
.
..
.
gesucht ist die waagrechte Strecke s unten
Mit tan(54) = h/s findet man sie.
in der Zeichnung ist
a2 + 2s = a1
so findet man die obere Kantenlänge und kann die Vol-Formel nun nutzen .
.
.
Nun zur Pyramide oben :
für die obere Pyramide wird der Winkel nicht gebraucht, denn
die Kantenlänge hast du ja vorhin berechnet , die Höhe ist 104-49
und die normal Vol-Formel für Py ist
1/3 * G * h