Geometriefrage (Kreis)
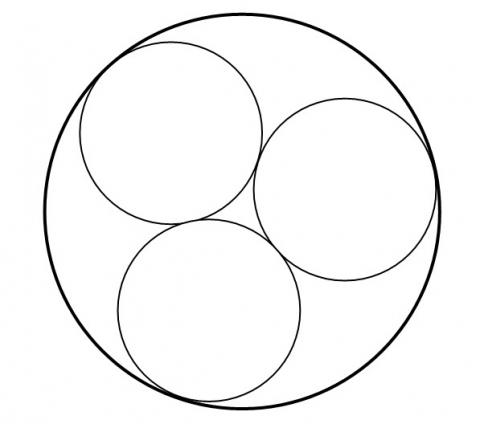
Hallo, kann mir bitte jemand eine Formel bzw. Berechnung für folgende Aufgabenstellung nennen: 3 gleichgroße Kreise (r = 3 cm) berühren sich gegenseitig. Das ganze System wird von einem vierten Kreis umschlossen (s. Skizze). Welchen Radius hat der 4. Kreis? Danke schon mal im Voraus.
8 Antworten
nochmal anders:mittelpunkte der 3 kreise verbinden ergibt gleichseitiges dreieck mit seitenlänge 6 cm und höhe ist h=a/2 mal wurzel 3 =3 mal wurzel 3 =5,196 jetzt davon 2/3 nehmen wegen schwerpunkt-strecken-verhältnis (höhen und schwerlinie sind ja hier dieselben) also 2/3 mal 5,196 =3,464, dann hast du entfernung von mittelpunkt des umkreises zu mittelpunkt eines kleinen kreises, also bis perepherie noch r=3 dazu ergibt dann R=6,464 gruß ej
Zu berechnen ist der Mittelpunkt des großen Kreises und der Abstand zur Kreislinie.
Dazu benötigen wir den Mittelwert der Mittelpunkte der kleinen Kreise (diese bilden ein gleichseitiges Dreieck mit der Kantenlänge 6 cm). Sei z.B. M1 = (0,0), M2 = (6,0) und M3 = (0,6); dann ist M' = (3,3). Der gesuchte Radius ist der Abstand von M' von einem der drei Punkt Mn + r (3cm). Der Abstand ist sqrt (18). Der gesuchte Radius ist also 3sqrt(2) + 3 cm, also ca. 7,24 cm.
Stimmt, der Fehler ist mir beim Essen auch aufgefallen. Die Mittelpunkte sind falsch bezeichnet. (0,0) und (6,0) geht noch, aber der dritte Punkt ist dann bei (3, 3 sqrt(3) ). M' ist dann der Punkt auf der Achse x=3, der von den Punkten M1, M2, M3 den gleichen Abstand hat. Also gilt: (3,y) hat vom Ursprung den Abstand sqrt(9+y²). Andererseits hat er vom M3 den Abstand 3 sqrt(3)-y. Die beiden Abstände sind identisch. Das Lösen der Gleichungssystems ergibt y=sqrt(3).
Somit ist der gesuchte Radius sqrt(12) [nicht 18] + 3 = 6,464 cm. Sorry für meinen Fehler.
mist wenn die editier Funktion zu schnell ausläuft
^^meinen Fehler schon entdeckt^^
@boriswulff: wo ist das Rechtwinklig das sind 3 anneinanderliegende Kreise die schon selbst ein Dreieck bilden, da kann nur ein Gleichseitiges bei rauskommen.(demnach alle winkel 60°)
Aus den Mittelpunkten der kleinen Kreise kann man ein gleichseitiges Dreieck zeichnen, das immer genau durch die Berührungspunkte von jeweils 2 Kreisen verläuft. Die Seitenlänge dieses Dreieckes ist 2r (der kleinen Kreise). Der Schnittpunkt der Winkelhalbierenden jeder Seite ergibt den Kreismittelpunkt des großen Kreises. Das kann man mit dem Pythagoras ausrechnen, weil es immer rechtwinklig auf die Gegenseite des Dreieckes trifft... So weiter verfahren mit allen Teilstrecken. Etwas umständlich, aber lösbar.
Antwort ist richtig, aber der Rechenweg zu umständlich. Der Mittelpunkt eines gleichseitigen Dreiecks lässt sich einfacher ermitteln - ist der Schwerpunkt der Figur, also die Summe der Ortsvektoren der drei Eckpunkte geteilt durch 3.
Du kannst hier ein Gleichseitiges Dreieck mit einer Seitenlänge von 12cm bilden.
Der Rechenweg zur berechnung des Umkreisradius ist demnach:
R = 12cm/ 2sin60
und laut meinem Taschenrechner ergibt das einen Umkreisradius von 6,93cm
http://de.wikipedia.org/wiki/Gleichseitiges_Dreieck
ich würde den umkreisradius des innenliegenden gleichseitigen dreickes berechnen....oder? zumindest würde ich dahingehend recherchieren.
Das Dreieck M1, M2, M3 ist allerdings hier nicht gleichseitig sondern rechtwinklig. Deswegen kann das ganze schon von Grund auf nicht so funktionieren.