Gauss Verfahren, wo liegt mein Fehler, denn ich komme nicht weiter?
Hallo,
ich habe folgende Aufgabe 2 mit Gauss gelöst, allerdings komme ich gar nicht mehr weiter und weiß gar nicht, wo mein Fehler liegt. Kann mir da jemand helfen? Ich würde mich so freuen.
VIelen Dank.
Marc
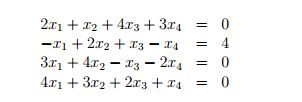
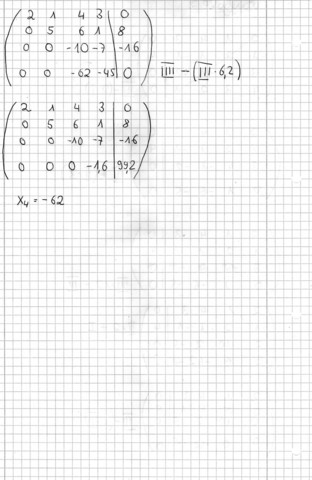

3 Antworten
Hallo,
ich habe mir angewöhnt, bei solchen Matrizen schematisch vorzugehen.
Zunächst notiert man nur die Koeffizienten, so wie Du es auch gemacht hast:
2 1 4 3 |0
-1 2 1 -1 | 4
3 4 -1 -2 |0
4 3 2 1 |0
Nun nehme ich mir die erste Spalte vor, wobei ich jede Zahl in dieser Spalte so mit der ersten Zahl der ersten Zeile, also mit 2, verrechne, daß als Summe eine Null entsteht.
Ich habe 2 und -1. Wenn ich die -1 mit 2 multipliziere und zu der 2 addiere, bekomme ich 2-2=0
Ich muß also die zweite Zeile mit 2 multiplizieren und zur ersten Zeile addieren.
So bekomme ich als zweite Zeile 0 5 6 1 |8
Die erste Zeile werde ich die ganze Zeit unverändert übertragen (auch wenn ich sie zwischendurch für die Verrechnung schon mal verändern werde)
Nun verrechne ich die dritte Zeile mit der ersten, wobei ich mich wieder an den jeweils ersten Zahlen der ersten und dritten Zeile orientiere,
also der 2 und der 3.
Wenn es geht, vermeide ich Brüche, weil ich die Zwischenschritte im Kopf zu rechnen pflege und nur jeweils die fertigen Matrizen nach jeder bearbeiteten Zeile notiere.
Ich rechne also 3*Zeile 1 minus 2*Zeile 3 und komme so auf
0 -5 14 13 | 0
Obwohl ich in Gedanken und für diese Rechnung die erste Zeile mit 3 mulitipliziert habe, schreibe ich sie dennoch unverändert auf.
Bei der vierten Zeile habe ich vorn eine 4 stehen. Wenn ich die 2 aus der ersten Zeile verdopple und davon die 4 aus Zeile 4 abziehe, komme ich auch hier auf eine Null. Das heißt: 2*Zeile1 minus Zeile 4:
0 -1 6 5 |0
Nun ist die erste veränderte Matrix fertig, die in der ersten Spalte drei Nullen besitzt:
2 1 4 3 |0
0 5 6 1 |8
0-5 14 13|0
0 -1 6 5 |0
Nun kommt die zweite Spalte dran.
Diesmal verrechne ich die Zeilen 3 und 4 jeweils mit Zeile 2. Zeile 1 ist aus dem Spiel und wird nur noch mitgezogen.
Dadurch, daß in der ersten Spalte 3 Nullen übereinanderstehen und nur noch die Zeilen 2,3 und 4 miteinander verrechnet werden, bleiben dort die Nullen erhalten. Das ist der Sinn dieses Verfahrens. Wenn Du etwa Zeile 3 mit Zeile 1 verrechnen würdest, um nun als zweite Zahl von Zeile 3 eine Null zu erhalten, wäre die erste Null in der Zeile wieder futsch, weil sie ja entweder zu der 2 aus Zeile 1 addiert oder von ihr subtrahiert würde und Du hättest nichts gewonnen.
So aber kannst Du die Zeilen 2 und 3 mit beliebigen Faktoren außer Null multiplizieren, ohne daß sich an der ersten Null etwas ändert.
Die jeweils zweiten Zahlen in Zeile 2 und 3 sind 5 und -5, was praktisch ist, weil sie sich schon zu Null addieren.
Ich rechne also einfach Zeile 2 plus Zeile 3 und erhalte als dritte Zeile (die zweite werde ich wie die erste für die nächste Matrix unverändert übernehmen):
0 0 20 14|8
Da alle Zahlen gerade sind, kürze ich direkt durch 2:
0 0 10 7 |4
Nun verrechne ich Zeile 4 mit Zeile 2:
Ich habe an zweiter Stelle wieder die 5 und die -1.
Also Zeile 2 plus 5*Zeile 4:
0 0 36 26 |8
Auch hier kürze ich wieder durch 2:
0 0 18 13 |4
Nun habe ich die dritte Matrix fertig:
Wie gesagt, lasse ich nun die Zeilen 1 und 2 aus Matrix 2 unverändert stehen:
2 1 4 3 |0
0 5 6 1 |8
0 0 10 7 |4
0 0 18 13|4
Nun bleibt uns nur noch, Zeile 3 und 4 zu verrechnen. Da an den beiden ersten Stellen dieser Zeilen Nullen stehen, bleiben sie beim Verrechnen erhalten.
Diesmal wird auch Zeile 3 in die endgültige Matrix unverändert aus Matrix 3 übertragen.
An dritter Stelle haben wir die 10 und die 18. Das kgV dieser beiden ist 90.
Ich muß also Zeile 3 mit 9 multiplizieren, Zeile 4 mit 5 und anschließend
Zeile 4 von Zeile 3 abziehen:
Zeile 4 lautet danach:
0 0 0 -2 |16
Wenn ich hier durch -2 kürze:
0 0 0 1 |-8
Wieder zusammenbauen, wobei Zeilen 1 bis 3 aus Matrix 3 übernommen werden:
2 1 4 3 |0
0 5 6 1 |8
0 0 10 7 |4
0 0 0 1 |-8
Die Stufenform ist fertig.
Für x4 kann ich die Lösung -8 direkt ablesen.
Ich setze diesen Wert in Zeile 3 ein:
10*x3+7*(-8)=4
10*x3=60
x3=6
Nun setze ich für x3 die 6 und für x4 die -8 in Zeile 2 ein:
5*x2+36-8=8
5*x2=-20
x2=-4
Nun die Werte für x2, x3 und x4 in Zeile 1 einsetzen:
2*x1-4+24-24=0
2*x1=4
x1=2
Die Lösung lautet also:
x1=2, x2=-4, x3=6, x4=-8
Das ist vielleicht nicht die schnellste Methode, um so ein System zu knacken, aber die Gefahr, Fehler zu machen, ist bei der Arbeit nach einem festen Schema geringer.
Du mußt nur mit den Vorzeichen aufpassen und Dir immer bewußt sein, ob Du gerade addierst oder subtrahierst.
Herzliche Grüße,
Willy
Ja, man kann sich schnell verrechnen. Das Lösen solcher Matrizen ist eine gute Konzentrationsübung.
Es gibt übrigens auch ein Verfahren, bei dem die Unbekannten durch Determinanten bestimmt werden. Das ist auch nicht schlecht.
Allerdings ist das bei einer 4x4-Matrix wie hier (ohne den Lösungsvektor) doch recht aufwendig, weil Du immer erst einmal Untermatrizen bilden mußt.
Bei einer 3x3-Matrix plus Lösungsvektor geht das aber wunderbar, weil Du hier die Determinaten über die Sarrus-Regel bestimmen kannst. Du brauchst insgesamt nur vier Determinanten für die drei Unbekannten bilden, was mit etwas Übung recht fix geht.
Ich hatte das Gauß-Verfahren früher überhaupt nicht richtig kapiert, weil mir nicht klar war, daß ich Zeilen so verrechnen muß, daß die ersten Nullen jeweils übereinanderstehen und daß ich z.B. die erste Zeile nicht jedesmal umschreiben muß. Ich hatte irgendwie wild herumgerechnet, bin dann irgendwie aufs Ergebnis gekommen - aber das Ganze hatte weder Hand noch Fuß.
Das lag natürlich auch daran, daß Du als Schüler mehr an Mädels als an Mathe Interesse hast oder am Unterricht allgemein und deshalb nicht immer so genau hinhörst, wenn der Lehrer etwas erklärt. Deshalb kann ich durchaus verstehen, wenn Schüler mit manchen einfach scheinenden Dingen so ihre Probleme haben.
Das ist die verbesserte version

Der (erste?) Fehler liegt schon bei der ersten Umformung vor III+(II*3) ergibt zwar die x1, x2, x3 aber als reine Zahl 12
Dieser Fehler pflanzt sich mehrfach fort.
habs verbessert. Ich lade gleich neue version hoch, moment.
hab jetzt die verbesserte version hochgeladen.
Guten Abend Willy, vielen Dank für die große mühe. Die Matrix habe ich gut gelöst in der zwischenzeit. allerdings fehlten mir die letzten schritte, die Matrix richtig zu lösen. Nun geht das ja so einfach. leichtes spiel, aber man muss genau rechnen und ohne fehler.