f(x)= 0,5*sin(x)+0,25=0
Hi,
ich muss bei dieser Gleichung exakte Koordinaten bestimmen. Habe nur keine Ahnung, wie man das schriftlich macht. Ich schreib euch mal die Aufgabe auf.
"Das Schaubild von f schneidet die Parallele zur x-Achse durch (0 | 0,5) in zwei Punkten. Bestimmen Sie die exakten Koordinaten."
Falls mir jemand das erklären sollte, dann bitte nicht nur die Lösung hinschreiben, sondern auch mit Rechenweg, da ich schlecht in Mathe bin.
Danke im voraus :)
2 Antworten
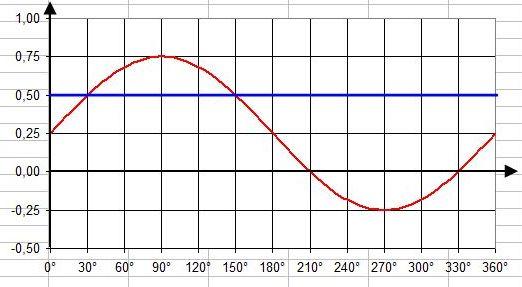
Die Parallele zur x-Achse durch (0 | 0,5) hat die Gleichung y = 0,5.
Setze also 0,5sinx + 0,25 = 0,5 → 0,5sinx = 0,25 → sinx = 0,5.
Dies hat im Bereich 0 < x < 360° die beiden Lösungen x = 30° und x = 150°
oder x = ⅙ π und x = ⅚ π.
Achso jetzt verstehe ich es, hätte nicht gedacht, dass es so einfach ist. Danke :)
Kann es auch mal passieren, dass die Lösung x größer als pi ist? Also x=3,4 usw. Oder sind sie immer kleiner als pi?
Es gibt unendlich viele (und beliebig große) Lösungen,
wenn man den Definitionsbereich nicht einschränkt.
zB mit ⅙π ist auch ⅙π ± 2π und ⅙π ± 4π usw Lösung.
Siehe Bild
(1) f(x) = 0,5 * sin(x) + 0,25
(2) f(x) = 0,5
(1) = (2) 0,5 * sin(x) + 0,25 = 0,5
sin(x) = 0,5 >>> x1 = 30°; x2 = 180° - 30° = 150°
