Funktion für Rechenturm?
Hallo, Community!
Ich habe heute meiner kleinen Schwester (1.Klasse) bei den Hausaufgaben geholfen und dabei sog. Rechentürme kennengelernt (s.u.).
Man hat die beiden unteren Zahlen gegeben und addiert dann halt immer. Kein besonderes Kunststück soweit, ich gebs zu, aber ich hab dann ein bisschen drüber nachgedacht und mir eine Frage gestellt, die wohl eher auf meinem schulischen Niveau ist...
Gibt es eine Funktion, einen Term, der die Zahl im oberen Stein ausrechnet in Abhängigkeit von den beiden unteren Zahlen und der Turmhöhe?
Ich habe jetzt schon eine zeitlang rumgerechnet und Regelmäßigkeiten gesucht, aber irgendwie komm ich nicht drauf... Also Mathe-Genies ans Werk!
8 Antworten
- Die n-te Zahl eines Turms
- mit der untersten Zahl a und
- der zweituntersten Zahl b ist
x(n) =
[ ((√(5) -1)a) / (2√(5)) +b/√(5) ] * [ (1+√(5))/2 ]^n +
[ ( 1/2 +1/(2√(5)) )a -b/√(5) ] * [ (1-√(5))/2 ]^n
Begründung: Die Zahlen des Turms sind Glieder einer rekursiv definierten Folge, die der gleichen Rekursionbedingung wie die Fibonacci-Folge unterliegt (siehe stekum). Alle diese Folgen bilden einen Vektorraum der Form
x(1, Φ, Φ², Φ³, Φ^4, ...) + y(1, Φ', Φ'² Φ'³ Φ'^4, ...),
wobei die Maßzahlen des Goldenen Schnitts
Φ = (1+√(5)) / 2, Φ' = (1-√(5)) / 2;
die Lösungen der charakteristischen Gleichung
1 + µ = µ²
und x, y die Koordinaten der jeweilige Folge bezüglich des von den oben bezeichneten Baisvektoren aufgespannten (zweidimensionalen) Koordinatensystems sind. - Für die mit a und b beginnende Folge ergibt die Auflösung des Gleichungssystems
- x + y = a
- Φx + Φ'y = b
die allgemeinen Koordinaten
x = ((√(5) -1)a) / (2√(5)) +b/√(5) und y = (1/2 +1/(2√(5)) )a -b/√(5)
der obigen Formel; für a = b = 1 kommt (mit etwas Vereinfachungs-Aufwand) die Formel von Binet heraus.
. . .
Probe: Vereinfache obige Formel für n = 1, 2, 3, 4, 5
Sehr gut. Mein Versuch, diese Formel nur mit Fibonacci(x) so allgemeingültig hinzubekommen, scheiterte an der Zeit...
Mit hypergerds Ansatz lässt sich die Formel von Binet ("Fibonacci(x)" bei hypergerd) direkt verwenden; das ist vielleicht etwas einfacher. Jedenfalls lässt sich an vielen Stellen die Symmetrei von Φ und Φ' verwenden. - Ich beschränke mich auf den Zahlenturm im Beispiel. Dieser hat mit der eigentlichen und einer verschobenen Fibonacci- Folge (siehe auch stekum) die Form:
3 * (1, 1, 2, 3, 5, 8...) - 2 * (0, 1, 1, 2, 3, 5, ....);
nun ist mit der Fomel von Binet (siehe z.B. im Wikipedia-Artikel "Fibonacci-Folge" unter "3.1 Formel von Moivre-Binet"):
(1, 1, 2, 3, 5 ...) = (Φ^n - Φ'^n) / √5, wobei
Φ = (1 + √5) / 2 und Φ' = (1 - √5) / 2.
Das ergibt für den Zahlenturm im Beispiel die Darstellung:
3 * (Φ^n - Φ'^n) / √5 - 2 * (Φ^(n-1) - Φ'^(n-1)) / √5 =
(1 / √5 ) [ 3 * (Φ^n - Φ'^n) - 2 * (Φ^(n-1) - Φ'^(n-1)) ] =
(1 / √5 ) [ 3 * Φ^n - 2 * Φ^(n-1) - 3 * Φ'^n + 2 * Φ'^(n-1) ] =
(1 / √5 ) [ (3 - 2 / Φ) Φ^n - (3 - 2 / Φ') Φ'^n ];
Nebenrechnung:
(3 - 2 / Φ) / √5 =
- mit 1 / Φ = 2 / (1 + √5) = 2(1 -√5) / (1 - 5) = - Φ'
(3 + 2 Φ') / √5 =
(4 - √5) / √5 = 4/√5 - 1
entsprechend:
(3 - 2 / Φ') / √5 =
(3 + 2 Φ) / √5 = 4/√5 + 1
eingesetzt:
x(n) = [ 4/√5 - 1 ] * [(1 + √5) / 2]^n - [4/√5 + 1] * [(1 - √5) / 2]^n ;
die Formel ist etwas einfacher als die, die bei Einsetzen von a = 3, b = 1 in die allgemeine Formel herauskommt (beachte: Die hier angegebene Fomel ist eine Differenz, die allgemeine Formel eine Summe):
Bleibt zu zeigen, dass sich die beiden Formeln für x(n) für a = 3 und b = 1 übereinstimmen.
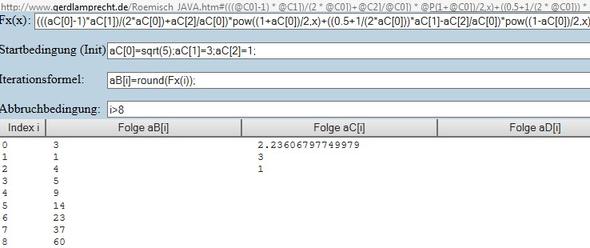
Habe mal die Formel von psychironiker an den Iterationsrechner übergeben:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#(((@C0]-1) * @C1])/(2 * @C0])+@C2]/@C0]) * @P(1+@C0])/2,x)+((0.5+1/(2 * @C0])) * @C1]-@C2]/@C0]) * @P(1-@C0])/2,x)@N@C0]=@Q5);@C1]=3;@C2]=1;@N@Bi]=round(Fx(i));@Ni%3E8@N0@N0@N#
(LINK endet mit N# und beinhaltet alle Formeln)
Ja, sie funktioniert und kann mit beliebigen untersten ganzzahligen Wert aC[1] und den darüber liegenden aC[2] berechnet werden.
siehe Bild
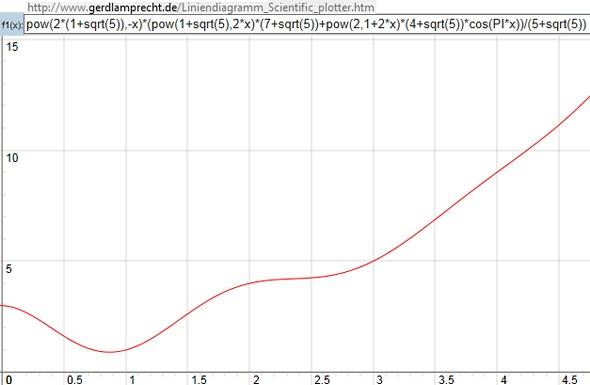
Die exakte explizite Formel lautet 3 * Fibonacci(x-1)+Fibonacci(x) =
pow(2 * (1+sqrt(5)),-x) * (pow(1+sqrt(5),2 * x) * (7+sqrt(5))+pow(2,1+2 * x) * (4+sqrt(5)) * cos(PI * x))/(5+sqrt(5))
Man kann sie sogar zeichnen siehe Bild
Gewöhnlich gibt es diesen Turm doch mehr als Pyramide. So wie deiner dargestellt ist, vermute ich jetzt auch nur, dass die dunklen Zahlen die gegebenen sind. Irgendwo müsste es noch eine Vorschrift geben, ob addiert oder subtrahiert werden soll. (Auch bei Addition wäre ja ein Ergebnis herausgekommen, es sei denn, es wäre als Bedingung mitgegeben worden, die oberste Zahl sollte die größte sein.)
Einen allgemeinen Algortihmus herzustellen, dürfte nur in Grenzfällen gelingen.