Extremwertprobleme ~ Mathematik
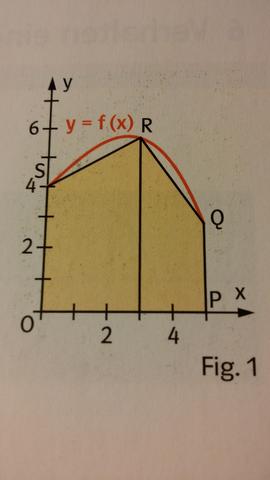
Erstmal zur Aufgabe: "Gegeben ist eine Funktion f mit f(x)= -0,05x³+x+4; 0≦x≦5. Die Punkte O (0/0), P(5/0), Q(5/f(5)), R(u/f(u)9 und S(0/f(0) bilden ein Fünfeck.
a) Benutze die Flächeninhaltsformel für Trapeze und zeige, dass sich der Inhalt dieses Fünfecks in Abhängigkeit von u mit der Formel A(u)=(1/2)(4+f(u))u+(1/2)(f(u)+2,75)(5-u) berechnen lässt. Gib eine sinnvolle Definitionsmenge an.
b) Für welches u wird der Flächeninhalt maximal?"
Ich komme mit der Aufgabe leider gar nicht zurecht und bräuchte schnell Hilfe, da ich diese schon bald vortragen muss.. Die Flächeninhaltsformel fürs Trapez wäre ja A= (1/2)(a+c)h und wäre somit der 2. formel sehr ähnlich.. dennoch verstehe ich nicht ganz was das u damit zu tun hat. Natürlich kann das Fünfeck je nach dem wo der Punkt R ist größer oder kleiner sein.. aber wie beweise ich dass diese Formel das nun auch berechnet?
Bild ist beigefügt ~
2 Antworten
Hallo LaObscura,
die angegebene Formel A(u) stimmt. Das kann man sehen, wenn man den Flächeninhalt der beiden Trapeze mit Deiner Formel A= (1/2)(a+c)h ausrechnet. Man muss dann alles ausmultiplizieren, einige Potenzen heben sich weg. Man erhält eine Funktion 3. Grades von u.
Um das maximale A zu bekommen, muss man die Gleichung nach u ableiten. Das ergibt eine quadratische Gleichung, deren Nullstellen man bestimmen muss. Als Lösung erhalte ich u=2.887 . Das ist nicht an der Stelle des Maximums der Kurve, sondern etwas rechts daneben.
Gruß von leiermann
stell doch mal die Formeln für beide Trapeze auf; beide haben als g =f(u) also u in f eingesetzt und linke Höhe h=u und rechte Höhe h= 5-u dann wirst du schon sehen, dass du auf das Ergebnis kommst.