Eine Punktladung Q wird auf einer Metallkugel/Isolator kugel angebracht wie ist die Kraft F?
Fragestellung ist
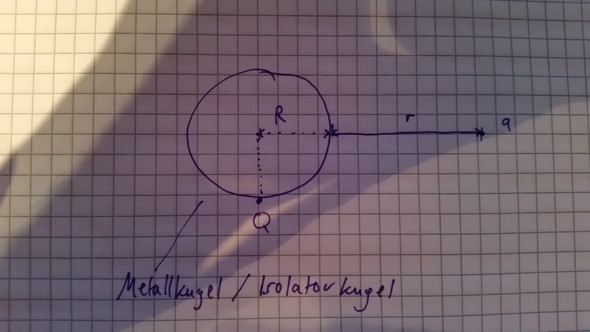
Eine Ladung Q werde wie skizziert auf bzw. in einer Kugel mit dem Radius R aufgebracht. Geben sie jeweils die Kraft (Betrag) an, die auf eine zweite Ladung q in der Entfernung r von der Kugeloberfläche wirkt
a) wenn die Kugel eine massive Metallkugel ist b) wenn die Kugel eine massive Isolator kugel ist
gesucht sind die Formeln für a und b.
2 Antworten
a) alles verteilt sich an der Oberfläche. Diese Verteilung ist radialsymmetrisch um den Ursprung, also ist der relevante Abstand
Reff = r+R
b) Die Ladung bleibt wo sie ist. Der relevante Abstand ist
Reff = √{ (R+r)²+R²}
Das ist kein üblicher Begriff und hab ich mir den nur ausgedacht weil ich die ganze Formel nicht hinschreiben wolle (Epsilon, 4*pi, usw). Es geht hier um den relevanten Abstand zur gedachten Ersatz-Punktladung. Einmal sitzt die unten auf der Kugeloberfläche, einmal im Zentrum der Kugel.
Einfach das Coulombgesetz verwenden. Der Abstand der Kugelmittelpunkte ist gleich dem Radius der großen Kugel.
Ob die Kugel aus Metall oder aus einem Isolator besteht, spielt keine Rolle.
Ob die Kugel aus Metall oder aus einem Isolator besteht, spielt keine Rolle.
Nein, im ersteren Fall verteilt sich die Ladung auf der Kugel, während sie im letzteren Fall an der Stelle bleibt.
Das ist richtig, wobei es auch beim Isolator zu leichten Ladungsverschiebungen kommt (dielektrische Polarisation).
Meines Wissens spielt das aber für die Kraft nach dem Coulombgesetz keine Rolle - oder wie würden Sie das sehen?
Die Ladungsverschiebung durch Influenz wird ja im Coulombgesetz nicht berücksichtigt. Die Frage ist, ob es sich mit diesem Ansatz um eine Vereinfachung handelt und man sie eigentlich berücksichtigen müsste. Da habe ich bisher noch nie etwas drüber gelesen bzw. noch nie tiefer drüber nachgedacht.
bei verschiebbaren Ladungen wird die Ladungsverteilung durch eine Probeladung verfälscht. Deshalb macht man diese auch immer infinitesimal klein, damit das nicht passiert.
Z.B. würde eine Probeladung q von einer ansonsten ladungsfreien metallischen Kugel angezogen werden, da sich die darauf befindlichen freien Ladungen verschieben. Dieser Effekt ist aber natürlich quadratisch in q. Ist die Gesamtladung der Kugel Q, kommt noch eine Anziehung dazu, die proportional zu Q*q ist, also linear in q. Der quadratische Anteil verschwindet im Limes kleiner Probeladungen.
Wieder was dazugelernt... Hatte außerdem fälschlicherweise angenommen, dass die Punktladung direkt an der anderen Kugel sitzt. Ist noch früh am Morgen :-)
Das mit dem effektiven Radius findet man in Standard-Schulbüchern nicht, wobei die Aufgabe ansonsten typisch für eine Schulaufgabe ist.