Casio fx-85DE Plus Gleichung lösen Dritten Grades
Fogendes zu meinem Taschenrechner ich brauche das demnächst. Ich muss mit meinem Taschenrechner beispielsweise die Funktion f(t)=0,008t^3-0,28t^2+2t+25,6 die Stellen berechnen an denen es f(t)=18 ergibt. Hoffe ihr könnt weiterhelfen wie ich das ganze machen kann. Habe in der Bedienungsanleitung nichts finden können.
2 Antworten
Dieser Taschenrechner ist ja wirklich sehr primitiv und ungenau :-(
Leider schriebst Du nicht, was Ihr in Mathe schon alles hattet (Klassenstufe usw.). Ich kann mir nicht vorstellen, dass der Lehrer für das Eingeben einer Aufgabe, die dann ein Rechner ausführt, Punkte/Noten bekommt...
Fast jeder hat doch ein internetfähiges Handy, und da kann man wie unter
http://www.lamprechts.de/gerd/php/gleichung-6-grades.php
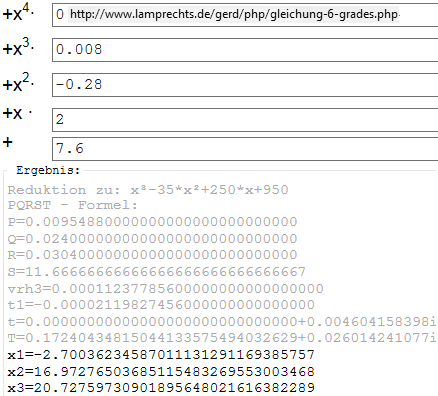
alles exakt auf bis zu 64 Stellen berechnen lassen (Cardanische Formeln oder PQRST-Formel ... siehe Bild)...
Lehrer vergeben auch selten Aufgaben, die so extrem "krumme" (irrationale) Ergebnisse haben. -> Schreibfehler?
Es sei denn, Ihr sollt absichtlich grafisch oder numerisch an die Sache herangehen: Bisektion, Newton-Verfahren, selbstkonvergierende Iterationsformeln...
Manchmal kommt man auch mit Substitution weiter, aber bei diesem Fall:
0=x³-35*x²+250*x+950 kommen komplexe Zwischenergebnisse -> und so etwas wie Imaginärteil hattet Ihr bestimmt noch nicht - oder?
x3=35/3+(95/(1/5 (-373+3*i*sqrt(3594)))^(1/3)+5^(2/3) *(-373+3*i*sqrt(3594))^(1/3))/3
um auf das Ergebnis im Bild zu kommen.
Da dein Rechner keine Nullstellenbestimmungsfunktion (SOLVE) hat, kannst du das nur "händisch" mit einem Näherungsverfahren machen, z.B. mit dem Newton-Verfahren.
Da die von dir angegebene Gleichung keine ganzzahligen Lösungen besitzt, geht es leider auch nicht mit dem Prinzip "erste Lösung erraten und abspalten".
Man kann kubische Gleichungen zwar auch exakt lösen, das ist aber wesentlich mehr Arbeit als das Newton-Verfahren.
Dann brauch ich wohl doch noch bis zur Zentralen Klausur nen neuen Taschenrechner xD Trotzdem Danke :D Wiedereinmal hat mein Mathelehrer nicht recht gehabt