Anwendungsaufgabe zum Satz des Pythagoras .
Ich schreibe mrgen eine Arbeit und bin gerade am üben,aber ich versteh diese eine Aufgabe nicht : Auf die Dachreling eines Pizza - Taxis sollen zwei rechteckige Platten für werbung aufgeschraubt und oben verbunden werden.Das auto mit dachreling ist 1,43 m hoch, die holme der dachreling sind 2,10 m lang und 1,39 m voneinander entfernt. Das auto soll unter einem 3,00 m hohen carport stehen . der sicherheitsabstand in der höhe soll 10 cm betragen. wie groß dürfen die platten höchstens sein ?
Wäre nett wenn ihr mir das erklären könntet. wenigstens den ansatz . bittte .
2 Antworten
Da ich vermute, dass du die Aufgabenstellung noch nicht so ganz verstehst (Denn sonst müsste dir eigentlich klar sein, wei du rechnen musst), mach ich ne neue Antwort auf, damit ich ein Bild einfügen kannn (Bitte nicht über meine Zeichenkünste lachen).
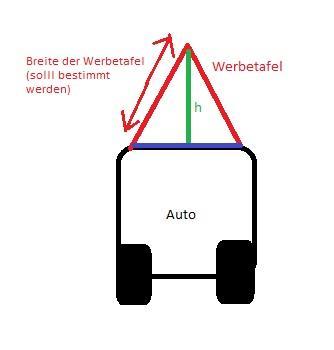
Auf dem Bild siehst du die beiden Werbetafeln. Die grüne Höhe h ergibt sich aus den Höhen und dem Sicherheitsabstand:
h=3,00m-1,43m -0,1m= 1,47m
Die blaue Linie ist die Breite des Autos, also 1,39m lang. Da das Dreieck aus roten und blauen Linien gleichschenklig ist, und die grüne Linie senkrecht auf der belauen Linie steht, gilt: die grüne Linie teilt die blaue Linie genau in der Mitte. Damit hat man aus dem großen Dreieck zwei kleinere Dreiecke gemacht, die jeweils aus einer roten Linie, einer grünen Linie und der Hälfte der blauen Linie bestehen. Da außerdem die grüne Linie senkrecht zur blauen ist gilt der Pythagoras mit:
rot²= (blau/2)²+grün² -->rot²=(1,39/2)² +1,47²=2,643
--> rot= √(2,643)≈1,63m
Damit dürfen die Platten maximal 1,63m breit sein.
Mach dir erstmal klar, wei das Ganze Aussieht: Die Platten werden nicht snkrecht angeschraubt, sondern "gekippt", sodass eine Art Dach entsteht. Stell die das so vor: Du und ein Helfer bringen jeweils deine Platte auf das Dach, d.h. die Unterkante der Platten ist bei 1,43 m, der Abstand von den Platten unten ist 1,39 m (Die Länge 2,10 wird nicht beenötigt). Jetzt lasst ihr beide eure Pallte los, sodass die nach innen kippen--> Dadruch bilden die ein Dach (Also gut, nder Realität wurden die bei der Art und Weise bloß auf das Autop krachen, aber ich denke du verstehst, was ich meine).
Damit hast du ein (gleichschneklicges aber nicht rechtwinkliges) Dreieck, dessen untere Seite 1,39 m lang ist und dessen andere beisden Seiten so lange sind, wie die Platten breit sind. Darasu kannst du jetzt sehr einfach zwei rechtwinklige Rechtecke machen, indem du einfach von der Spitze senkrecht nach unten gehst. Die Länge dieser geddachten Linie kannst du ja leicht aus den gegebenen Höhen und dem Sicherheitsabstand berechnen. Dann solte der Rest kein Problem mehr sein. Falls dochj, nochmals melden (Dann bitte genau erkläern, wo du nicht mehr weiterkommst)
danke , aber ich versteh nicht ganz wie breit die anderen beiden seiten sollen.wie kommt man darauf ?