Kann jemand dieses Problem lösen?
Ich habe erst kürzlich dieses Plakat entdeckt, und ich komme einfach nicht auf die Lösung. Hat es damit zu tun, dass man wenn man zwei Dreiecke berechnet einen Punkt doppelt zählt?:
(Das Bild konnte nicht geladen werden, deshalb beschreibe ich das Problem hier:)
Die drei Punkte A(0/5), B(-12/0) und C(0/0) definieren ein rechtwinkliges Dreieck. Die Kathete a misst also 12 Einheiten. Die Kathete B misst 5 Einheiten. Nach dem Satz des Pythagoras misst die Hypothenuse also 13 Einheiten. Teilt man nun allerdings die Kathete bei Punkt D (-7/2) In zwei Dreiecke auf (Dreieck BDE(-7/0) und Dreieck ADF(0,2), und berechnet die jeweiligen Hypotenusen dieser Dreiecke sind diese bei BDE Wurzel aus 5^2 + 2'2 und bei ADF Wurzel aus 7^2 + 3^2. Addiert man diese beiden Hypotenusen erhält man nicht wie man annehmen würde, die gleiche Länge wie die der Hypothenuse des grossen Dreiecks 13, sondern 13.000938. Wie lässt sich dieser Widerspruch auflösen?
4 Antworten
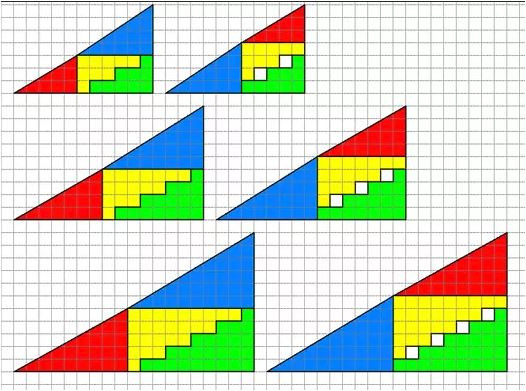
ungenau ist das bild. eine optische Täuschung , das ist alles.
so was in dieser Richtung.
Irgendwo fehlt was oder ist zuviel , man sieht es nur nicht sofort.
http://forum.computerschach.de/cgi-bin/mwf/topic_show.pl?tid=572
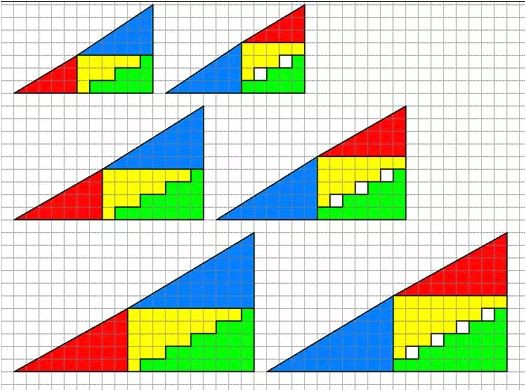
Errechne den Winkel von B anhand des großen Dreicks und zeige dass die Hypothenuse nicht exakt durch den Punkt (-7;2) läuft.
Geht auch mithilfe von linearen Funktionen
y = (5/12 )*x + 5
so lautet die Gleichung zwischen -12/0 und 0/5
bei x = - 7 sollte der Wert 25/12 sein.
in der Graphik ist er aber exakt 2
y = (5/12 )*x + 5
so lautet die Gleichung zwischen -12/0 und 0/5
bei x = - 7 sollte der Wert 25/12 sein.
in der Graphik ist er aber exakt 2 .
Die Graphik ist schief.
Punkt D (-9,2) liegt nicht auf der Verbindung AB.