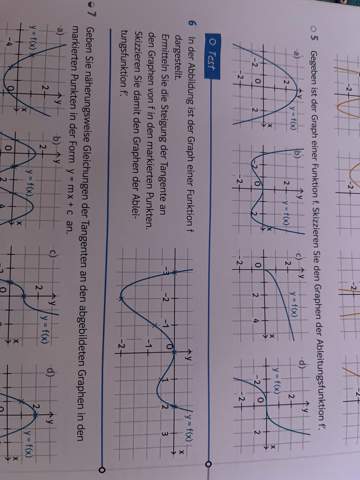
Ableitung und Tangenten?
Ich stehe bei Aufgabe 6 auf den Schlauch. Ich verstehe nicht wie ich da anfangen soll.
3 Antworten
Da gibt es zwei Möglichkeiten:
1) graphische Lösung: man zeichnet per Geodreieck die Tangente an den Graphen in den gesuchten Punkten und liest über ein Steigungsdreieck die Steigung ab. Diesen Wert trägt man in das Koordinatensystem ein. An den Extrema (1 Hoch-, 2 Tiefpunkte) muss der Graph von f' die x-Achse schneiden. Dann verbindet man die Punkte durch eine Kurve. Ob die Kurve über oder unter der x-Achse verlaufen muss, sieht man daran, ob die Steigung des Graphen positiv oder negativ ist.
2) Rechnerische Lösung.
Wir haben 4 Nullstellen gegeben bei x = -3; 0 (doppelte Nullstelle); 2
und setzen die Nullstellenform an:
f(x) = ax^2(x + 3)(x -2)
und formen das durch ausmultiplizieren zur Normalform um:
f(x) = ax^2 (x^2 + 3x - 2x -6) = ax^2(x^2 + x -6)
Nunmüssen wir noch a ermitteln und suchen uns dazu einen beliebigen Punkt aus, der gut ablesbar ist und sich gut rechnen lässt, z.B. P(1/-0,5) und setzen den ein:
f(1) = -0,5 = a(1 + 1 - 6)
-0,5 = -4a
a = 1/8 = 0,125
Damit erhalten wir:
f(x) = 0,125x^2(x^2 + x -6) = 0,125x^4 + 0,125x^3 - 0,75x^2
Das können wir nun ableiten:
f'(x) = 0,5x^3 + 0,375x^2 - 1,5x
Um es genau zu machen, ermitteln wir noch die Extrema des Ableitungsgraphen:
f''(x) 1,5x^2 + 0,75x - 1,5
und setzen das zu 0:
1,5x^2 + 0,75x - 1,5 = 0
x^2 + 0,5 - 1 = 0
pq-Formel:

f'(-1,281) = 1,49
f(0,781) = -0,71
Und stellen nun eine Wertetabelle auf:

Diese Punkte übertragen wir in ein Koordinatensystem und zeichen dann sinnvoll die Kurve:
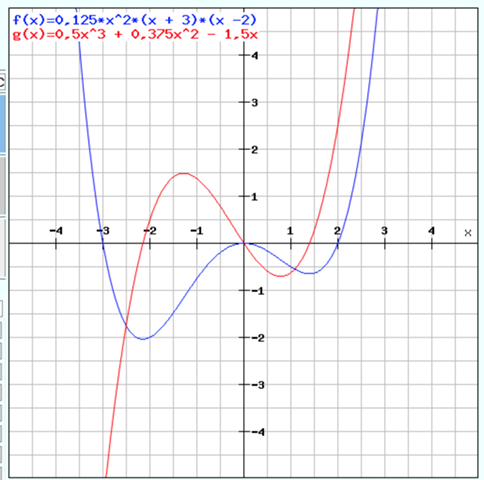


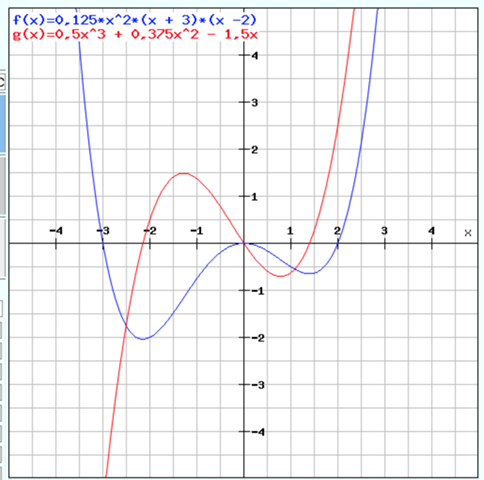
f(x)=((1)/(8)) (x^(4)+x^(3)-6 x^(2)) ist die funktion
du musst die Ableitungen der markierten Punkte finden und damit den Graphen der Ableitungsfunktion konstruieren.