Wie muss ich an die Aufgabe rangehen?
f(x)=90×0,87^x
x= Zeit in Jahren
90= der Baum war 90cm groß während er eingepflanzt wurde
0,87= wachstumsgsw
'Berechnen sie, wann die wachstumsgeschwindigkeit 50cm pro Jahr beträgt'
4 Antworten
Der Graph:
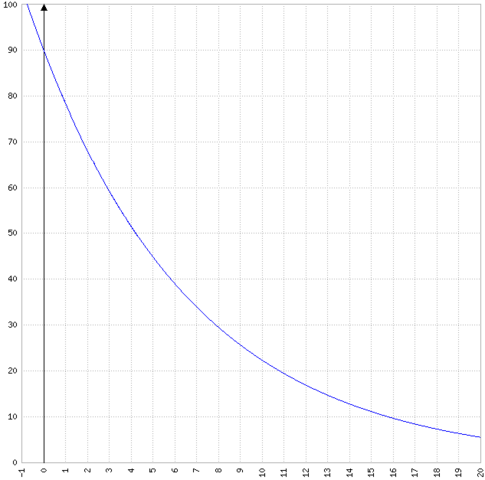
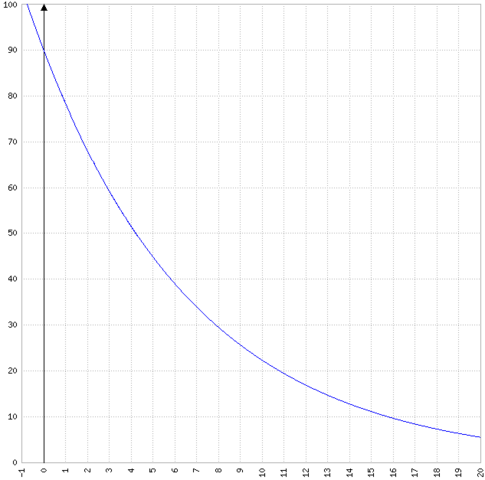
Jetzt versehe ich es. Es geht nicht um das Absolute Wachstum sondern um die Geschwindigkeit des Wachstums. Also wächst der Baum immer langsamer.
double a=50.0/90.0;
double x = Math.Log(a)/ Math.Log(0.87);
x= 4.2207233897689838
Etwas verwirrend, aber ich verstehe es so...
f(x)=90×0,87^x --> Im Jahr x beträgt das Wachstum f(x) = y cm
90=90×0,87^0 --> Im Jahr 0 beträgt das Wachstum 90 cm (Jahr der Pflanzung)
78,3=90×0,87^1 ---> Im Jahr 1 beträgt das Wachstum 78,3cm
~68,1=90×0,87^2 ---> Im Jahr 2 beträgt das Wachstum ~68,1cm
usw...
50=90×0,87^x --> Im Jahr x beträgt das Wachstum 50cm, x = ?
Er wird bei dieser Aufgabe davon ausgegangen, dass das Wachstum des Baums Jahr für Jahr abnimmt. Es wäre jetzt also für f(x) = y = 50 cm durch Umstellung de Gleichung der Wert für x zu ermitteln. Dabei könnte zwar ein krummer Wert herauskommen (Kommazahl), aber dann müsstest du die nächste Ganzzahl angeben für das Jahr, z.B. bei 5,4 wäre es demnach das 6. Jahr (Im sechsten Jahr beträgt das Wachstum...).
Warum 90x und nicht 90+ wenn
der Baum war 90cm groß während er eingepflanzt wurde
?
Ich weiß es leider nicht. Die Funktion steht so im Buch.
Was soll den f(x) ausdrücken? Die Größe? Für x=0 Jahre würde es ja stimmen, aber mit x=1 gebe es ein negatives Wachstum.
Den Wachstum, wenn ich es richtig verstanden habe
Und wie kann man es berechnen? Ich habe durch ausprobieren auch einen ungefähren Wert von 4,2 raus, aber ich möchte es berechnen und das genaue Ergebnis haben. Ist halt der Operator