Was ist der Unterschied zwischen Polstelle 1. und 2. Grades?
Gebiet: Analysis
2 Antworten
Ich ergänze und verallgemeinere die Anwort von rumar:
Es geht darum, wie oft der entsprechende Linearfaktor im Nenner eines Funktionsterm vorkommt. Beispiel:
x^4 - x³ - 3x² + x + 2
f(x) = ----------------------------------
x^5 - 7x³ + 2x² + 12x - 8
Zerlegt man Zähler und Nenner in Linearfaktoren, erhält man:
(x-1)(x+1)²(x-2)
f(x) = ------------------------
(x-1)²(x+2)²(x-2)
An diesem Term kann man gut die Definitionslücken ablesen: -2; 1, 2.
Kürzen des Funktionsterms ergibt:
(x+1)²
f(x) = --------------
(x-1)(x+2)²
Der Faktor (x-1) kommt im Nenner 1 mal vor, der Faktor (x+2) doppelt; damit hat f bei x=1 einen Pol 1. Grades, bei x=-2 einen Pol zweiten Grades.
Bei Polen ungeraden Grades hast Du dann einen VZW, hat ein Pol einen geraden Grad, liegt kein VZW vor.
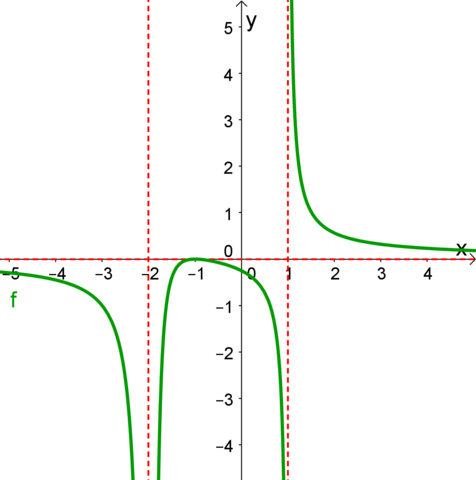
Einfachste Beispiele: Die Funktion f mit f(x) = 1/x hat an der Stelle x = 0 einen Pol ersten Grades bzw. erster Ordnung. Die Funktion g mit g(x) = 1/x^2 hat an der Stelle x = 0 einen Pol zweiter Ordnung. Graphischer Unterschied: Bei Polen ungerader Ordnung gibt es einen Vorzeichenwechsel (quasi einen "Sprung von + ∞ nach - ∞ " oder umgekehrt). Bei einem Pol gerader Ordnung gibt es keinen Vorzeichenwechsel.