Summe der vierstellige Zahlen?
weise nach, dass für jede vierstellige Zahl z mit untereinander und mit 0 verschiedenen Ziffern gilt:
die Summe aller vierstelligen Zahlen, die jeweils aus allen 4 Ziffern der Zahl z bestehen, is ein Vielfaches der Quersumme der Ausgangszahl z.
3 Antworten
Das liegt daran, das jede Ziffer an jeder Stelle gleich oft vorkommt.
Betrachten wir mal eine Zahl der Ziffernfolge abcd, dann heißt das ja Nichts anderes als
1000*a+100*b+10*c+d
Betrachen wir alle Permutationen von abcd, dann kommt jede der Ziffern an jeder Stelle genau 3!=6 mal vor. Das liegt daran, das jede Reihnenfolge der übrigen Ziffern eine andere Zahl ist. Betrachtet man die Wertigkeit, so ergibt sich für jede Ziffer ein Faktor von 6*(1000+100+10+1)=6666. Somit ist die Summe aller möglichen Zahlen aus den Ziffern gerade 6666 mal die Summe der Ziffern.
Hi,
da ist es so wie bei der 3stelligen Zahl war, nur diesmal isst die magische Summe 6666 (nicht 222)! :-)
also die Summe ist 6666 * Quersumme).
Wenn Du die Argumentation bei der vorherigen Aufgabe versstanden hast, dan ist diese naheliegend.
LG,
Heni
Hi,
hier noch eine kleine Tabelle als Stütze, damit Du meine erste Antwort vielleicht leichter verstehst:
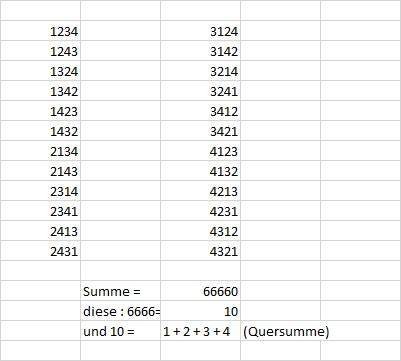
LG,
Heni
