Sägezahnfunktion in GeoGebra darstellen?
Hallo,
wie kann ich die bekannte Sägezahnfunktion in Geogebra darstellen? Ich weiß, dass es vordefinierte Programme gibt, aber ich möchte das gerne selber hinbekommen, weil ich dann mit der Funktion noch weiter arbeiten möchte.
Ich habe bisher nur die Funktion f(x)=pi/x im Bereich -pi<x<pi dargestellt bekommen. Nun müsste sich die Funktion nur noch peridoisch wiederholen...
1 Antwort
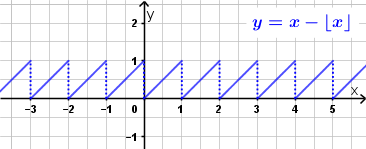
Man könnte sowas wie x - floor(x) machen.
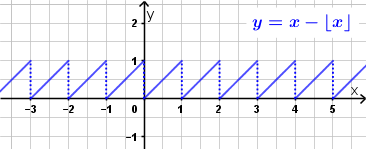
Das könnte man dann gegebenenfalls je nach Bedarf noch weiter anpassen.
============
Ich habe bisher nur die Funktion f(x)=pi/x im Bereich -pi<x<pi dargestellt bekommen.
Bist du dir sicher, dass du „f(x) = pi/x“ meinst? Das ist nicht so sägezahn-mäßig, da man da unter anderem auch eine Polstelle in jeder Periode hat. Aber sowas könnte man dann beispielsweise so machen...
f(x) = π/(x-2π*floor((x+π)/(2π)))
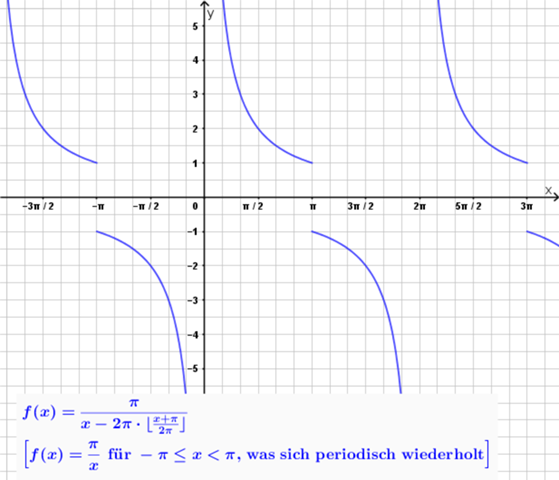
Allgemein, wenn man eine Funktion f(x) für a ≤ x < b hat und das periodisch wiederholen möchte...
f(x-(b-a)*floor((x-a)/(b-a)))
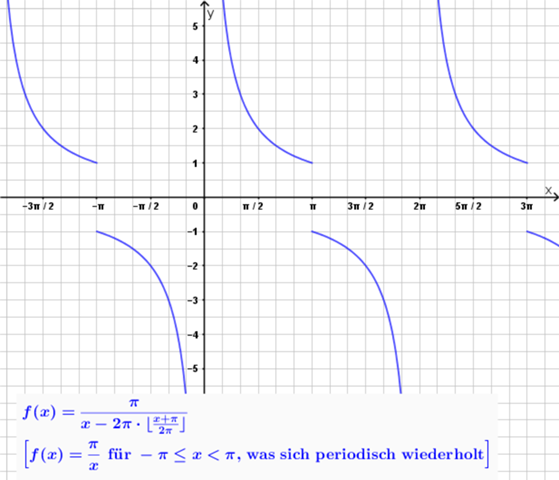
Naja. Die senkrechten, gestrichelten Linien sind sowieso eigentlich nur bedingt sinnvoll. (Schließlich gehören die ja nicht zum Funktionsgraphen, wenn man es genau nimmt.) Mathematisch gesehen, wäre die folgende Darstellung wohl etwas sinnvoller:
https://cdn.discordapp.com/attachments/882681362505695252/984830265908146216/sawtooth.png
===============
Wie dem auch sei. Für das Bild in meiner Antwort habe ich da einfach zusätzlich entsprechende Strecken zeichnen lassen:
Sequence(Segment((k, 1), (k, 0)), k, -10, 10)
Ich habe GeoGebra bei mir auf Englisch gestellt. Auf Deutsch kann man ...
Folge(Strecke((k, 1), (k, 0)), k, -10, 10)
... benutzen.
Da könntest du dann beispielsweise...
(x-2π*floor((x+π)/(2π)))/π
...oder ein klein wenig vereinfacht...
x/π-2*floor((x+π)/(2π))
... nutzen.
>Man könnte sowas wie x - floor(x) machen<
Die Eingabe stellt in Geogebra die ansteigenden Geraden dar. Wie bringt man das Programm dazu, auch die senkrechten (strichlierten) Linien zu zeichnen?