Quadratische Funktion Tunnel berechnen?

Moin Zusammen, ich benötige Hilfe bei dieser Zeichnung... Kann mir jemand relativ einfach erklären, wie ich hier X ausrechnen kann, wenn ich nur einen weiteren Wert habe?
- Ich bin lange aus der Schule raus und es sind nicht meine Hausaufgaben - ich begreife das nur einfach nicht und würde mein Wissen gerne erweitern.
Hab die Frage eigentlich nur nochmal gestellt, weils Teil der heutigen Aufgaben war.
4 Antworten
Es ist tatsächlich so, dass hier noch Angaben fehlen (trotz der inzwischen gelöschten, unqualifizierten Kommentare).
Zur Veranschlichung habe ich mal 2 quadratische Parabeln gezeichnet, da wird es wohl deutlich:
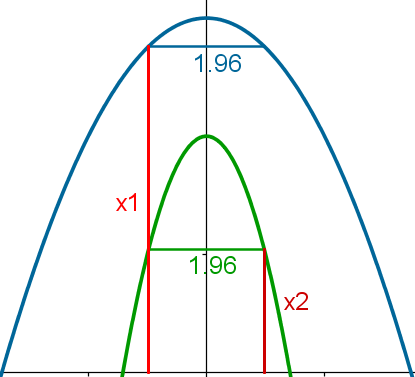
Die gleiche Breite ist in sehr unterschiedlichen Höhen zu finden.
Es fehlen noch Angaben wie Breite am Boden, maximale Höhe des Tunnels..., damit könnte man die entsprechende Funktion bestimmen und dann x ausrechnen.

Für diese Aufgabe werden die Achsen am besten so gewählt, dass die Symmetrie des Tunnels maximal ausgenutzt werden kann.
Das Maximum liegt somit auf der y-Achse und die beiden sog. Nullstellen (quasi die Endpunkte des Tunnels in diesem praktischen Fall) jeweils gleich weit von der y-Achse entfernt.
Ist eine Breite b der Brücke und eine Höhe h der Brücke gegeben, lässt sich die Funktionsgleichung innerhalb zwei einfacher Schritte herleiten.
1.
ist die faktorisierte Form der Funktionsgleichung unter Verwendung der Breite, der sog. Streckfaktor a hängt von der Höhe h ab. Die Höhe h führt zu den Koordinaten des Hochpunktes H(0|h).
2.
Eingesetzt in die Funktionsgleichung ergibt sich
und somit die Funktionsgleichung
mit x der Breite und f(x) der Höhe des Tunnels. Wir suchen anschließend die Höhe X auf der Zeichnung an der Stelle 0,96 (hier als Notiz wichtig: Die y-Achse verläuft durch die Mitte des 2D-Tunnels, weshalb die 1,92 in 2*0,96 aufgetrennt wird.).
Solche Rechnungen sind interessant, wenn bsp. herauszufinden ist im Sachkontext, ob ein LKW der Breite x die zugehörige Höhe f(x) nicht überschreitet.
Wir setzen also f(0,96) ein, damit wir die Höhe an dieser Stelle erhalten.
und erhalten mit dieser Rechnung die gesuchte Höhe X
Normalerweise muss zu diesem Beispiel eine Funktionsgleichung angegeben werden oder zumindest eine Höhe und Breite des Tunnels.
Sind diese Werte gegeben, ergibt sich daraus eine Funktionsgleichung der Form
f(x)=ax²+bx+c
Im besten Fall verläuft die y-Achse durch die Mitte des Tunnels, die x-Achse entlang der Fußenden.
Dann werden einfach die Funktionswerte an den Stellen 0,96 und -0,96 bestimmt, das Ergebnis ist die Höhe X.
Bitte, wenn möglich, einmal die komplette Aufgabenstellung mit allen Angaben nachlegen.
b ist zwar 0, aber da kein einziger Punkt gegeben ist,
ist die Aufgabe nicht lösbar.
Das ist doch schon mal eine vernünftige Aussage. Vielen Dank dafür! Ich hake da noch einmal nach, da mich das i.wie nicht in Ruhe lässt.
Grüße
Das wäre sehr gut. Wenn diese Größen gegeben sind, ist die Lösung ein 5-Zeiler.
Vieleicht gehst du Doch Lieber nochmal In die Schule🙂👍😅
Ja aber ich Stalke nicht 1000 Leute und Mache Diese Erfahrung auch öffentlich
Groß und Kleinschreibung - bitte! Die hellste Kerze scheinst du nicht zu sein - kommt sicherlich vom Haftschaden und dem dazugehörigen Seife fallen lassen, als du 14 warst.
Und falls du dir die Richtlinien durchgelesen hast dann müsstes du wissen das man andere leute nicht Demütigen darf also.....
Süß.
Vieleicht gehst du Doch Lieber nochmal In die Schule🙂👍😅
Gelesen hast du das aber schon, ja?
Also ganz ehrlich hab kein Bock mehr auf diesen Kindergarten hier schönen Tag dir noch
Ohhhh bist du sauer weil deine Antwort von den Mods gelöscht wurde? 😂
Nein - aber wollte das noch gerne loswerden.
Heul Doch
Adrian. Ach Adrian. Du bist auf mehreren Ebenen unterlegen - sieh es ein.
Haben doch gerade erst angefangen.
Die Idee mit dem Schaubild als Veranschaulichung finde ich super!