Mathematikaufgabe Parabel?
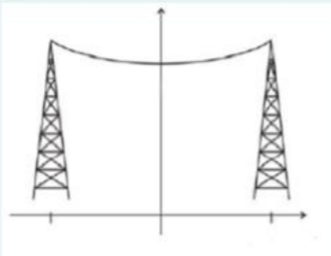
Ein Ingenieur muss eine Hochspannungsleitung bauen. Zwei Strommasten stehen 118 m voneinander entfernt, sie sind beide 236 m hoch. Vom Material des Kabels weiß man, dass es in der Mitte 20 m in die Tiefe hängen wird. Berechne die Öffnung der Parabel und gib dein Ergebnis möglichst genau ein.
1 Antwort
Leider hat dein Mathematiklehrer im Physikunterricht nicht aufgepasst. Der Durchhang eines freihängenden Seiles oder Kette folgt einer Kettenlinie (oder Seilkurve). Diese wird mathematisch durch den cosh beschrieben. Das ist definitiv keine Parabel!
Die Aufgabe ist nicht lösbar, denn es ist nicht möglich, den Verlauf der Leitungen mit einer Parabel zu beschreiben.
https://de.wikipedia.org/wiki/Kettenlinie_(Mathematik)#Parabel
Den Öffnungswinkel kann man aber dann doch berechnen. Das ist allerdings ein wenig umständlicher. (Alle Formeln mit Ausnahme der Ableitung aus obigem Link; die Ableitung kommt hier her https://www.gut-erklaert.de/mathematik/kettenregel-ableitung.html)
Mit w als Abstand zwischen den Türmen und h als Durchhang kannst du mit dieser Formel die Seillänge berechnen

damit und mit dieser Formel berechnest du der Krümmungsradius am tiefsten Punkt des Seiles

Damit hast du alles was du brauchst, um die Seilkurve mit dieser Formel zu berechnen

Um die Öffnung (den Öffnungswinkel) zu berechen
benötigst die Ableitung davon an der Stelle der Pfosten. Diese stehen bei x=w/2 bzw. bei x=-w/2 wobei Xo=0 ist. Damit ist die Steigung der Kettenlinie am rechten Pfosten
dy/dx = sinh(w/2a)
Die Steigung ist als Meter Höhe pro Meter Entfernung berechnet. Damit ist der Winkel zur Senkrechten der ArcusTangens des Kehrwertes davon und der Öffnungswinkel der beiden, durch die Seilköpfe gebildeten, Schenkel das Doppelte von diesem Winkel (die Linke Seite ist ja genau so wie die rechte Seite, nur anders rum)
Die Seillänge L=126,74m
Der Krümmungsradius a=90,39m
Die Steigung dh/dx = 0,7000
Der Öffnungswinkel gamma=110,01°
Wenn dein Mathelehrer fragt warum, dann bitte ihn, seinen früheren Kollegen Leibniz zu befragen. Eventuell kann auch Herr Huygens, Herr Bernoulli oder Herr Guttenberg helfen(siehe Link1). Vielleicht tut es auch ein fröhlicher Nachmittag mit dem Physiklehrer eurer Schule.



Danke, das muss ich sicher meinen Matheprofessor mitteilen