Mathe;Extremalprobleme

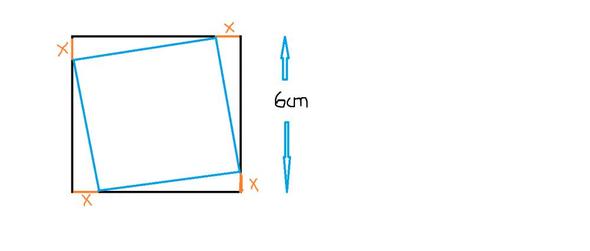
In einem Quadrat mit der Seitenlänge 6 cm wird von jedem Eckpunkt aus eine Strecke x abgetragen. Für welche Länge x hat dieses Quadrat minimalen Flächeninhalt?

Vorab,ich weiß nie ,ob ich meine Bedingungen richtig aufstelle bzw wie ich mal auf nen grünen Zweig da komme :( ...,also hab ichs mal auf verschiedene weisen probiert und ich wäre sehr dankbar ,wenn ihr mir sagt ,ob die richtige dabei ist und falls alles totaler müll ist wie ich den richtigen weg angehe :)

1. 
   24= 4y-4x /+4x
   * 24 = 4 Seiten á 6 cm...

   24 + 4x = 4y / :4

   6+ 1x = y
   A= x*y A=x(6+1x)

2. 24=2x-2x+2y-2x
Aufteilung in x und y seite ,was eigentlich schwachsinnig ist,weil ja in nem quadrat alle seiten gleichlang sind.....

3) 36= 4y-4x /+4x

36+ 4x = 4y / : 4

9+4x=y
A= x(9+4x)

A=9x + 4x ²

Answer 1

[hendih]

die Zielfunktion ist -2x²+12x Davon die Ableitung = -4x+12 Aufgelöst nach x= 3

Die Hauptbedingung: Flächeninhalt Innen = Flächeninhalt Gesamt - Flächeninhalt außen

Nebenbedingung: Flächeninhalt außen = -4x+12. aufgelöst nach ist das Ergebnis x=3

Dies setzt man in die Stammfunktion => -2x²+12x.

Für x wird 3 eingesetzt => Flächeninhalt außen = 18.

Dies subtrahiert man nun von Flächeninhalt Gesamt (6*6 = 36)

=> Flächeninhalt Innen = Flächeninhalt Gesamt - Flächeninhalt Außen

Flächeninhalt Innen = 18

Answer 2

[Aurel8317648]

b...Seite des neuen Quadrates

Pythagoras: b² = x² + (6-x)²

Fläche A = b² soll minimal werden, also Ableitung A ' = 0

A ' (x) = 2x + 2 * (6-x) * (-1) = 0 =>

x = 6 / 2 = 3

Comments

[Julezyxc]

nach meiner rechnung kommen für x = 6 raus

un wenn man die 6 von der anfangslänge abzieht kommt x= 0