Mathe Problem Nullstellenberechnung f(x) = x3 - 6x2 +8x?
Ich muss die Nullstellen dieser Funktion berechnen: f(x) = x3 - 6x2 +8x (Zahlen hinter x sind Exponenten kann keine Hochzahlen machen denn ich schreibe mit dem Handy) Ich habe es mit Faktorisieren, mit Substitution und mit Polynomdivision probiert. Weiß jemand auf welche Art ich wie die Nullstellen errechne? (Bin eine Mathe Niete 😭)
4 Antworten
Also wie ich es machen würde: x ausklammern dann wäre es xmal (x2-6x+8) und dann wäre es (x-4) mal (x-2) also sind die Nullstellen x=0 (vom anfang) und x=4 und x=2....hoffe ich zu mindest :D aber frag besser noch jemand anderen um sicherzugehen
ausgeklammert hab ich auch. x=4 und x=2 sind auch richtig (lösung steht Im Buch ) aber ich komm da nicht writer bei Mir kommt immer x2-x=3/4 raus
f(x) = x3 - 6x2 +8x
bei den nullstellen ist ja f(x)=0 -->
0=x3 - 6x2 +8x
also die erste nullstelle ist doch easy: einfach mal x ausklammern:
0= x(x^2-6x+8)
--> x1 =0
"ein produkt wird immer null, wenn einer der faktoren null wird", also:
0=x^2-6x+8
dann die lösungsformel und fertig ;)
du hast zu kompliziert gedacht mit substituieren, also:
immer wenns geht erstmal ausklammern...
?? wo ist dann des problem?!??
die lösungsformel ist:
x12= (-b+/- [wurzel] b²-4*a*c)/2a
also: x12= 6+/-[w]36-4*1*8)/2
x12= (6+/-2)/2
x1=(6+2)/2=4
x2=(6-2)/2=2
Hol dir Photomath für dein Smartphone. Die App kann die kompliziertesten Gleichungen lösen und erklärt jeden einzelnen Schritt.
Hoffe dass es verständlich ist :)
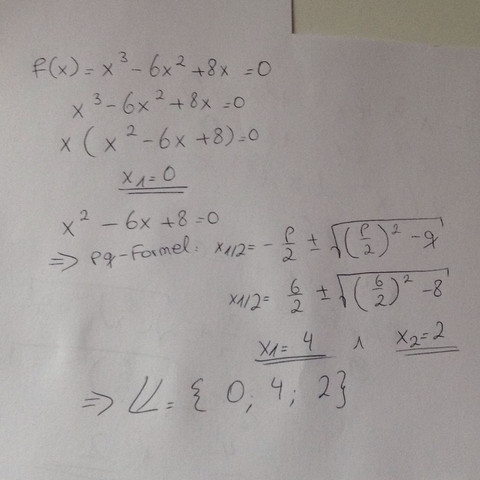
Da ist mein Fehler. Ich hab in die p/q Formel 6 anstatt -6 eingetragen Danke
soweit war ich auch schon