Kreisteile 5 Kreise mit Quadrat umschrieben?
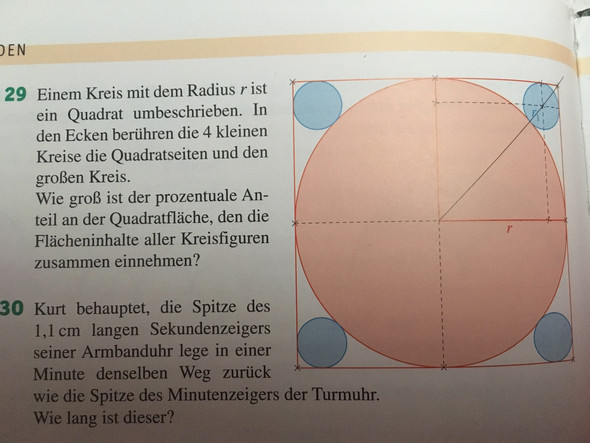
Ich komme in Mathe nicht weiter hier die Aufgabe: Einem Kreis mit dem Radius r ist ein Quadrat umbeschrieben. In den Ecken berühren die 4 kleinen Kreise die Quadratseiten und den großen Kreis. Wie groß ist der pozentuale Anteil an der Quadratfläche, den die Flächeninhalte aller Kreisfiguren zusammen einnehmen?
Bitte um nützliche Hilfe...
4 Antworten
Halbe Diagonale des Quadrates D/2 = r •√2 = r + r1(1+√2)
r1 = r • (√2-1) / (√2+1) | • (√2-1)/(√2-1)
r1² = r² • (3-√8)/3
Fläche des Quadrates Aq = 4r²
Fläche der Kreise Ak = π • r² + 4 • π • r² • (3-√8)/3
Ak/Aq = π • (1/4+(3-√8)/3) = 0,965 = 96,5%
Die Flächeninhalte des Quadrats und des großen Kreises sollten klar sein, oder? Um herraus zu finden wie groß die kleinen Kreise sind, solltest du dir mal das Dreieck in der Zeichnung ansehen (gestrichelte Linie), die Katheten haben jeweils die Länge r-r₁ und die Hypothenuse hat die Länge r+r₁. Mit dem Satz des Pythagoras kannst du r₁ und anschließend den Flächeninhalt der kleinen Kreise berechnen.
Zur Beantwortung der Frage muss zunächst der Radius r1 der kleinen Kreise ermittelt werden. In der vorliegenden Zeichnung sind bereits die erforderlichen Hilfslinien eingezeichnet, nämlich die Diagonale des Quadrats vom Quadratmittelpunkt (er sei M genannt) durch den Mittelpunkt des kleinen Kreises (er sei M1 genannt) zur Ecke des Quadrats (sie sei A genannt). Außerdem der waagrechte Radius von M zur rechten Seite des Quadrats.. Dieser Schnittpunkt des Radius mit der rechten Quadratseite sei S genannt, der Schnittpunkt der gestrichelten Linie von M1 senkrecht nach unten mit diesem Radius sei F genannt.
Dann gilt aufgrund der Ähnlichkeit zwischen Dreieck M-M1-F und Dreieck M-A-S die Beziehung MM1/MF = MA/MS
(r + r1)/(r - r1) = r*Wurzel(2)/r = 1,4142
r + r1 = 1,4142r - 1,4142r1
r1 = r(1,4142 - 1)/(1,4142 + 1)
r1 = 0,1716r
Damit ist (r1)² = 0,029436r²
Die 5 Kreise haben die Fläche Ak = r²pi + 4(r1)²pi = r²pi*(1 + 4*0,029436)
Ak = r²pi*1,1177 = r² * 3,5097 (pi = 3,14)
Ihr Anteil an der Quadratfläche beträgt also
3,5097r²/(4r²) = 0,8774 = 87,74%
Der Anteil des großen Kreises am Quadrat beträgt mit pi = 3,14
3,14r²/(4r²) = 0,785 = 78,5%
Von den 4 Lücken mit 21,5%, die der große Kreis frei lässt, füllen also die kleinen Kreise noch 87,7% - 78,5% = 9,2% aus und es bleiben immer noch 100% - 87,7% = 12,3% der Quadratfläche frei.
Die Fläche des Quadrats beträgt = (2 x r) x (2 x r)
Die Fläche des großen Kreises beträgt (((2 x r)²) x Pi) / 4
Berechnung der Fläche der kleinen Kreise:
Nebenrechnungen (Satz des Pythagoras): (r²) + (r²) = x
Wurzel aus x = y
y - r = Durchmesser eines kleinen Kreises
Durchmesser der kleinen Kreise / 2 = r₁ (Diese Rechnung ist nicht unbedingt notwendig, da man für den Flächeninhalt der kleinen Kreise auch gleich mit dem Durchmesser rechnen kann siehe unten)
Jetzt kann man den Flächeninhalt der kleinen Kreise ausrechnen:
((2 x r)² x Pi) / 4 = Flächeninhalt für einen kleinen Kreis (oder anders gerechnet = Durchmesser eines kleinen Kreises x Pi / 4)
Flächeninhalt für einen Kreis x 4 = Flächeninhalt aller kleinen Kreise ( Anmerkung: Zur Vereinfachung kann man natürlich auch im voherigen Schritt das / 4 einfach weg lassen und hat dann gleich den Flächeninhalt aller 4 kleinen Kreise)
100 / Flächeninhalt des Quadrats x Flächeninhalt aller Kreise = Prozentualer Anteil aller Kreise an der Quadratfläche.
Als kleiner Zusatztipp: Das Ergebnis sollte bei ca. 92 % liegen. Ich habe eben mal selbst gerechnet. Bei meiner Rechnung bin ich von Pi = 3,14 ausgegangen.
Sehe gerade noch einen kleinen Fehler
((2 x r)² x Pi) / 4 = Flächeninhalt für einen kleinen Kreis (oder anders gerechnet = (Durchmesser eines kleinen Kreises)² x Pi / 4)
sorry
Hinweis: Bei der Berechnung von r1 hat sich ein Fehler eingeschlichen. Richtig ist r1 = r*(3 - Wurzel(8)) und
(r1)² = r² * (3 - Wurzel(8))²