Ist diese Quadratische Gleichung unlösbar?
x^2-8x+16=0
5 Antworten
Ist diese Quadratische Gleichung unlösbar?
Nein, definitiv nicht!
x² - 8x + 16 = 0
Da solltest du direkt sehen, dass man hier die pq-Formel anwenden kann.
Wichtig: Je nach Bundesland werden andere Lösungsverfahren genutzt. Falls dir die pq-Formel also nichts sagt, sollten dir Mitternachtsformel oder ABC-Formel etwas sagen.
Du hast nun also:
x² - 8x + 16 = 0
Setzten wir das in die (pq-) Formel ein, erhalten wir folgende Nullstelle:
x = 4
Die Nullstelle ist also N(4 | 0).
Das kannst du auch im Bild noch einmal sehen und gut erkenne.
Eine weitere Lösung erhalten wir nicht, weil der Radikand bzw. die Diskriminante, also das, was unter der Wurzel steht, 0 wird.
Dafür kannst du dir folgendes merken:
Wird die Diskriminante positiv, erhalten wir 2 Lösungen.
Wird die Diskriminante 0, erhalten wir 1 Lösunge.
Wird die Diskriminante negativ, erhalten wir keine Lösung.
Das gilt für die pq-Formel!
Hier findest du noch einmal ein Video zur pq-Formel, wo auch das erklärt und erläutert wird:
https://youtube.com/watch?v=IM7qCdUyFh4
Liebe Grüße
TechnikSpezi
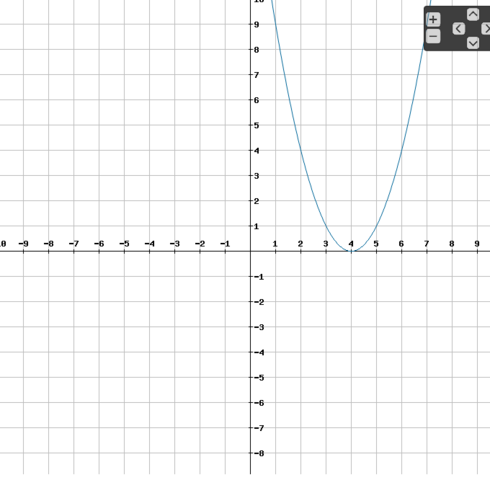
0=x^2 - 8 *x +16 Nullstelle bei x=4
Parabel nach oben geöffnet und berührt die x-Achse
Scheitelkoordinaten xs= - (a1)/(2*a2) und ys= - (a1)^2/(4*a2) + ao
a2=1 und a1= - 8 und ao=16
Nein, durchaus nicht. Es ist die binomische Formel zu
(x-4)^2.
Daraus erhältst Du:
x = + 4
Allerdings hat diese Gleichung (im Gegensatz zu vielen anderen quadratischen Gleichungen, die zwei Lösungen haben) nur diese eine Lösung.
4 +- sqrt(16-16) = 4 +- 0. Also eine ein-eindeutige Lösung.
Wurzel aus 0 ist 0, weil 0² = 0
Schau mal genau hin! Tipp: Binomische Formel