Höhe einer quadratischen Pyramide berechnen?
Hallo ich muss die Höhe einer quadratischen Pyramide berechnen gegeben sind mir leider nur Seite a mit 6m und ein Winkel mit 30grad kann mir jemand helfen ?
7 Antworten
Berechne d mit Pythagoras:
d²= 6² + 6²
-> d= 6* Wurzel(2)
h bekommst du nun mit einer Winkelbeziehung heraus, z.B. mit Sinus:
sin(30)= h/(d/2) I*(d/2)
->(d/2)*sin(30) = h
->h = 2,1213
Zuerst mal rechnest du d aus:
sqrt(a²+a²)=d
Dann weiter mit dem Tangens:
tan 30°=h/0,5d
mal 0,5d
-->
tan 30° *0,5d=h
Verstanden? ;)
Viele Grüße
yunatidusauron
Dafür muss eine trigonometrische Gleichung aufgestellt werden.
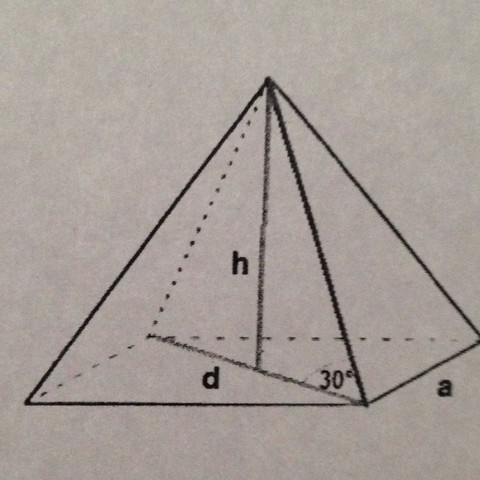
Es exisitiert ein rechtwinkliges Dreieck zwischen der unteren Grundflächenecke, der Spitze der Pyramide und ihrem Grundflächenmittelpunkt.
Die Längen des rechtwinkligen Dreiecks sind die Höhe der Pyramide, die Seitenkante und Hälfte der Grundflächendiagonale.
Der Winkel zwischen Seitenkante und Grundflächendiagonale beträgt genau 30°.
Die Höhe h der Pyramide ist die Gegenkathete zum gegebenen Winkel, die Hälfte der Grundflächendiagonale d die Ankathete.
Also kannst du eine Gleichung aufstellen:
tan 30° = h/(d/2) = 2h/d
Nun muss noch die Grundflächendiagonale berechnet werden.
Dies ist mit dem Satz des Pythagoras möglich:
a² + a² = d²
2a² = d²
d = √(2a²) = a√2
d = 6m * √2 = 6√2m
Jetzt muss die erste Gleichung durch eine Äquivalenzumformung nach h aufgelöst werden:
tan 30° = 2h/d |*d
tan 30° * d = 2h |:2
h = tan 30° * d/2
Nun noch Einsetzen in die vorherige Gleichung:
h = tan 30° * d/2
= tan 30° * 6√2m/2
= tan 30° * 3√2m
= √3/3 * 3√2m
= √3√2m ≈ 2,45m
Die Pyramide ist daher etwa 2,45m hoch. ;)
Ich hoffe, ich konnte dir helfen; wenn du noch Fragen hast, kommentiere einfach.
LG Willibergi
tan 30 = h / (d/2) ► h = (d/2) • tan 30
d mit Pythagoras berechnen.
Tip:Pythagoras und der Sinussatz helfen dir weiter. Schau ins Tafelwerk und denk erstmal nach. Danach - melde dich wieder.
tan(30)=h/(d/2)