Funktion in Python darstellen?



So wie es im Titel lautet. Ich mache irgendwas falsch aber weiß nur nicht was, kann mir jemand weiterhelfen?
Das mit der Asymptote usw. ist mir gerade nicht wichtig. Ich möchte nur die Funktion richtig darstellen können…
Was genau funktioniert nicht wie erwartet? Der Graph sieht auf den ersten Blick korrekt aus.
Wenn ich den Graphen in GeoGebra eingebe sieht er nicht so aus. Eigentlich ist die Funktion ja für x=-1 gar nicht definiert, jedoch zeigt es bei meinem Graphen nicht so an.
1 Antwort
Eigentlich ist die Funktion ja für x=-1 gar nicht definiert, jedoch zeigt es bei meinem Graphen nicht so an.
Ich hatte verstanden, die Asymptote sollten wir ignorieren; nun ja.
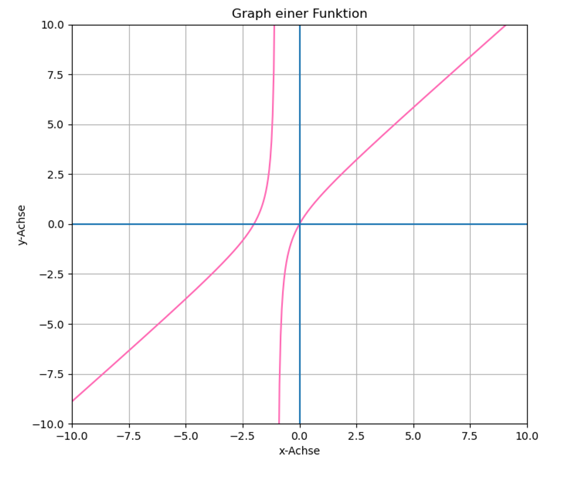
Das Problem hier ist, dass Matplotlib in solchen Plots Kontinuität annimmt und ungestört durch eine Asymptote interpoliert, wenn der kritische Wert nicht betrachtet wird. Das ist hier der Fall (unabhängig von x[x != -1]). Geben wir den linspace x direkt nach print, ist die Ausgabe folgende:
[…] -1.07769424 -1.02756892 -0.97744361 -0.9273183 […]
Das, obwohl mit 400 Schritten zwischen -10 und 10 natürlich exakt -1 getroffen werden sollte. numpy verwendet unter der Haube hier jedoch Gleitkommazahlen (siehe x.dtype); der linspace ist dann so konstruiert, dass ein Schrittwert berechnet wird, durch welchen die Elemente aufgebaut werden (Quellcode). Damit einhergehend ist jedoch die Genauigkeitsproblematik bei Gleitkommazahlen: https://en.wikipedia.org/wiki/Floating-point_arithmetic#Accuracy_problems. -1 ist schlichtweg übersprungen worden. x[x != -1] würde, wenn es das -1 Element gäbe, eine Division durch null verhindern, aber auch wieder das Interpolations-Problem verursachen!
Um mit Mengen mit fehlenden oder fehlerhaften Daten zu arbeiten, gibt es in numpy "Masken": https://numpy.org/doc/stable/reference/maskedarray.generic.html#rationale
Mit einer solchen lässt sich folgendes Ergebnis erzielen:

import matplotlib.pyplot as plt
import numpy as np
import numpy.ma as ma
def f(x):
return (x**2 + 2*x) / (x +1)
x = np.linspace(-10,10,400)
# https://numpy.org/doc/stable/reference/routines.ma.html#to-a-masked-array
x = ma.masked_values(x,-1, rtol=0.02,atol=0.02)
plt.plot(x,f(x), color='hotpink')
plt.xlim([-10,10])
plt.ylim([-10,10])
plt.axvline(0)
plt.axhline(0)
plt.title("Graph einer Funktion")
plt.xlabel("x-Achse")
plt.ylabel("y-Achse")
plt.grid()
plt.show()
GeoGebra tut dies automatisch anhand einer Heuristik. Das ist aber nicht genau! Es können bei so ziemlich jedem Plot fehlerhafte Darstellungen entstehen, welche nur durch rigorose Berechnungen erkannt und mitigiert werden können. Eine Grafik ist kein Beweis.
—
Alternativ kannst du auch zwei linspaces konstruieren, einen von -10 bis -1 und einen von -1 bis 10, und separat auf dasselbe Plot plotten. Numpy Arrays stören sich dabei nicht an Divisionen durch null; gibt nur einen Hinweis in der Konsole.
x^3 -2x^2-5x+6 sieht mir erst mal wie eine komplett andere Funktion aus; mit der Darstellung in Python hat Polynomdivision und Ähnliches jedenfalls nichts zu tun. Vielleicht handelt es sich hier um eine andere Aufgabe?
Weißt du vielleicht, ob es irgendwie eine Regelung gibt, dass man gebrochene Funktionen zuerst „umformen“ muss bevor man sie in Python darstellt.
Nun ja, gebrochen (rationale) Funktionen sind bis auf Lücken in der Domäne / Definitionsmenge recht artig; eigentlich kann dabei nur Division durch null schiefgehen. Dazu musst du in den Nenner schauen und ermitteln, ob und durch welche Werte in Variablen (sofern es keine 0 als Konstante gibt) Nullen entstehen können. Genauer kann das Verfahren, denke ich, nicht beschrieben werden.
Tools wie WolframAlpha spucken dir das aus (meist in Mengenschreibweise. Hier z. B. {𝑥 ∈ ℝ : 𝑥 ≠ -1}), aber wenn du es handschriftlich machen sollst, kann es je nach Komplexität auch einfach etwas Arbeit bedeuten.
Sprich doch sonst noch einmal mit der Lehrkraft. Solche Fragen zeigen, dass du dich bemühst, und sind oft aufschlussreich!
Wow vielen Dank für die ausführliche Nachricht, war echt hilfreich!
Weißt du vielleicht, ob es irgendwie eine Regelung gibt, dass man gebrochene Funktionen zuerst „umformen“ muss bevor man sie in Python darstellt.
Meine Freundin hat nämlich bei der Aufgabe bzw. bei der Funktion zuerst (glaube ich) eine Polynomdivision durchgeführt sodass sie die Funktion x^3 -2x^2-5x+6 erhält.