Funktion 3.Grades Problem
Hallo Community,
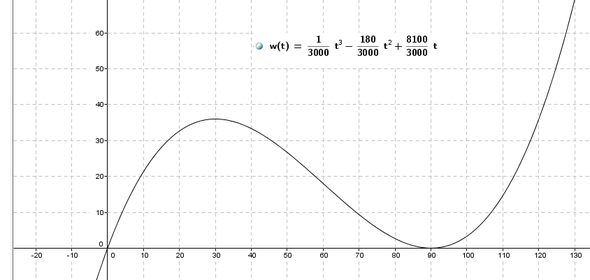
ich habe ein Problem mit einer Funktion 3. Grades. Ich schreibe nächste Woche eine Klausur darüber und hänge bei der Übungsaufgabe fest. w(t)=1/3000t^3 - 180/3000t^2 + 8100/3000t
So ich habe die Funktion in ein Koordinatensystem gezeichnet(siehe Bild) und bei Aufgabe 2 steht nun folgendes: "Beschreiben Sie das Wachstum der Hopfenpflanze anhand des Verlaufs des Graphens, nennen Sie dabei drei charakteristische Merkmale" und Aufgabe 4 "Berechnen sie den Zeitpunkt, an welchem die Wachtumsrate der Hopfenpflanze maximal ist und geben Sie den dazugehörigen Wert der Wachstumsrate zu diesem Zeitpunkt an.
Ich möchte nicht die Lösung wissen, sondern bräuchte Hilfe wie ich den Weg zur Lösung finde.
Mit freundlichen Grüßen Goebii
2 Antworten
Steht w(t) für Wachtum in Abhängigkeit von der Zeit t? Es macht natürlich einen Unterschied, ob die Funktion die Höhe des Hopfens oder das Wachstum angibt.
Wenn das Wachstum gemeint ist, musst Du bei 2) entsprechend den Graphen beschreiben. Kann es sein, dass t <= 90 gilt? Da ist das Wachstum ja wieder null. (Das war schon ein charakteristisches Merkmal.)
Bei 4) ist dann schlicht das Maximum zu berechnen. Nach Graph liegt ein rel. Maximum bei t = 30, was Du rechnerisch bestätigen musst. Die zugehörige Wachstumsrate ist dann der y-Wert. Du musst aber einen sog. Randwertvergleich machen, denn es kann ja durchaus sein, dass es am Rand des Def.-Bereiches einen höheren y-Wert gibt, nur dass dort kein rel. Maximum existiert. Der höchste dieser y-Werte ist dann Deine Lösung.
Ganz simpel berechnet man ja immer im Vertrauen auf die Folgerichtigkeit einer solchen Aufgabe den Extremwert mit
f'(t) = 0
Bei so eindeutiger Graphik entfällt dann sogar die Kontrolle mit f", sofern die Werte jenseits von 90 Tagen nicht relevant sein sollten. Ein weiteres Maximum gibt es ja nicht.
Vielen Dank, das macht Sinn bei 2. Dann ist ja der P(0/0) auch einer. Also muss ich bei Aufgabe 4 eine Ableitung machen und deren Schnittpunkt mit der X- Achse zeigt mir den Xwert an wo der Hochpunkt ist.(Hoffe das versteht man was ich meine)