Beweis von diesem Ausdruck?
Hallo ihr Lieben! Sitze gerade an einer Aufgabe für Analysis 1, die mich etwas verzweifeln lässt. Uns wurde der Tipp gegeben, dass man für den Beweis verwenden kann, dass x über k nichts anderes ist als (x/k) * (x-1) über (k-1). Leider habe ich nicht mal einen Ansatz..
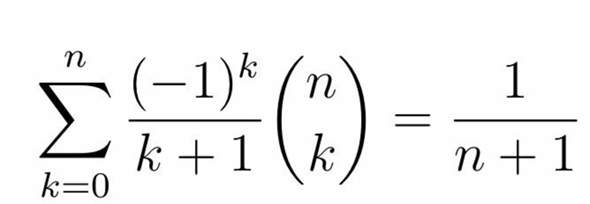
2 Antworten

Du erweiterst den Bruch mit (n+1). Dann ziehst du 1/(n+1) vor die Summe (ist ja nicht von k abhängig).
Dann hast du da stehen:
1/(n+1) * Summe von k = 0 bis n (-1)^k * (n+1)/(k+1) * (n über k).
Jetzt musst du "nur noch" zeigen, dass diese neue Summe gerade gleich 1 ist.
Dazu wendest du den Tipp an:
Summe von k = 0 bis n (-1)^k * (n+1)/(k+1) * (n über k)
= Summe von k = 0 bis n (-1)^k * (n+1 über k+1)
Jetzt verschiebst du die Indizes:
= Summe von k = 1 bis (n+1) (-1)^(k-1) * (n+1 über k)
Das sieht doch schon verdächtig nach dem binomischen Lehrsatz aus, fehlt nur leider der Wert für k = 0, macht aber nix, den zieh ich wieder ab:
= Summe von k = 0 bis (n+1) (-1)^(k-1) * (n+1 über k) - (-1)^(0-1) * (n+1 über 0)
= Summe von k = 0 bis (n+1) (-1)^(k-1) * (n+1 über k) - (-1) * 1
= Summe von k = 0 bis (n+1) (-1)^(k-1) * (n+1 über k) + 1
In meiner Summe fehlt stört mich das k-1 im Exponenten, das hole ich mal heraus
= (-1) * Summe von k = 0 bis (n+1) (-1)^k * (n+1 über k) + 1
Jetzt weiß ich, das 1 hoch irgendwas immer noch 1 ist und das schreib ich mal passend hin
= (-1) * Summe von k = 0 bis (n+1) 1^(n+1-k) (-1)^k * (n+1 über k) + 1
Und schon steht da der binomische Lehrsatz für (1-1)^(n+1):
= (-1) (1-1)^(n+1) + 1
Und das ist
= (-1) (0)^(n+1) + 1 = 0 + 1 = 1.
Mit dem obigen ist also alles gezeigt.


DAS geht mit vollständige Induktion.
