Ableitung transzendenter Funktionen, Anwendungsbeispiele??

Hallo zusammen,

hier eine Aufgabe bei der ich nicht weiter komme.

Bei Bedarf kann ich sie auch gerne übersetzen.

The intensity of illumination of light from a source varies directly as the cosine of the angle of incidence, and inversely as the square of the distance r from the source. How high above the center of a circle of radius 10 in. should a light be placed so that the intensity at the circumference will be a maximum.

Ich habe lediglich den Text so interpretiert:

$I=k\frac{\cos\left(θ\right)}{r^2}$

und

$h=\sqrt{r^2-100}$

sollte ich

$\frac{dh}{dθ}$ berechnen?

Danke für eure Kommentare.

Answer 1

[GreenxPiece]

Ich würde das so angehen:

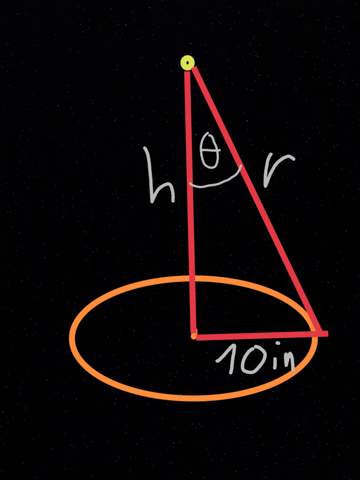
Skizze hilft immer. I = k cos(θ)/r^2 stimmt schonmal. Wobei ich k als I0 bezeichnet hätte. Ist aber wohl Geschmackssache.

Du brauchst eine Funktion I(h) um I in Abhängigkeit von h zu maximieren. Dazu muss man cos(θ) und r durch h darstellen.

cos(θ) = h/r

r = wurzel(h^2 + 100 in^2)

Damit ist

I = f(h) = (h/wurzel(h^2+100))/(h^2+100)

Also:

Umformen, Ableiten und 0 setzen ergibt für I ein maximum bei h = 7,07 inch

PS: deine Überlegungen sind nicht ganz sinnig. Zur aufgabe: Du hast eine Größe I, die in Abhängigkeit von einer Größe h maximiert werden soll. Zu berechnen ist also dI/dh = 0. Also musst du auf eine Form kommen die das differenzial dI/dh zulässt. dh/dθ wie du es geschrieben hast macht da keinen Sinn. Daher ist auch h = wurzel(r^2-100) nicht zielführend.

Comments

[usmi49]

Hallo GreenxPeace,

beim Umformen bekomme ich $I=kh\sqrt{\left(h^2+100\right)}$

dabei erhalte ich nicht die Ableitung von hier oben?

[GreenxPiece]

@usmi49

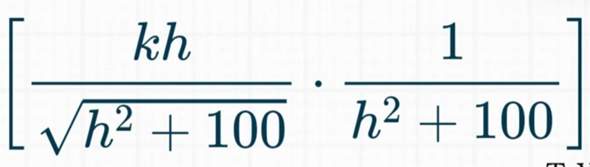
Achtung (h^2+100) muss in den Nenner. Der große bruchstrich ist der zweite. Also

f(h) = (h/wurzel(h^2+100))/(h^2+100)

So musst du rechnen.

[usmi49]

@GreenxPiece

$I=k\frac{h}{\frac{\sqrt{h^{2+100}}}{h^{2+100}}}=k\frac{h\left(h^2+100\right)}{\sqrt{h^2+100}}=k\frac{h\left(h^2+100\right)\left(\sqrt{h^2+100}\right)}{\left(\sqrt{h^2+100\ }\right)\left(\sqrt{h^2+100}\right)}=kh\sqrt{h^2+100}$

Ist das falsch?

soll es

$I=\frac{\left(\frac{h}{\sqrt{h^2+100}}\right)}{h^2+100}$ sein ?

Ja ich denke so sollte es aussehen weil cos θ = h/r oder ?

[usmi49]

@usmi49

Also das k hatte ich noch vergessen. Mit Umformen komme ich dann zu deinem Ausdruck hier oben.

Vielen Dank.

[usmi49]

Hallo GreenxPeace,

danke für deine Antwort.

die Skizze hatte auch so gemacht aber bin trotzdem nicht weiter gekommen.

Ich dachte fälschlicherweise dh/dθ weil h sich auch verändert bei Änderungen von θ.