Wie beweist man das und was bedeutet es überhaupt?
Hallo alle miteinander,
ich stehe vor dieser Matheaufgabe und ich weiß leider nicht, was einige von diesen Sachen bedeuten:
Wir befinden uns im Teilgebiet der linearen Algebra und ich soll dies beweisen:
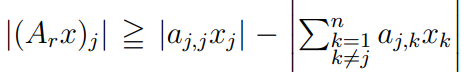
wobei A_r eine gegebene Bandmatrix ist für geeignete 1<= j <= 39. Ich weiß nicht was das a bedeutet.
Als Hinweis solle man sich die gegebene Matrix A_r veranschaulichen und explizite Werte für x einsetzen (beispielsweise eine Teilmatrix von A_r für x einsetzen).
Was bedeutet k ≠ j und wie ist das Komma aufzufassen? Wie sieht die Summe ausgeschrieben aus ? Und warum steht bei a nur ein Buchstabe (j) und nicht zwei wie a_(j,i) (das ist die eigentliche Schreibweise für ein Element aus der Matrix) ?
Welchen Beweisschritt soll man da angehen ? (Ich tendiere zur vollständigen Induktion).
Ich verstehe auch nicht, wie ein Komma mitten im Betrag stehen kann. Wie rechnet man damit ?
Eine etwas ausführlichere Erklärung wäre sehr nett.
Vielen Dank im Voraus für die Antworten.

Aufgabenstellung:
Gegeben sei folgende Matrix A_r ∈ R^(39 x 39).
*Matrix dargestellt* *eine Zahl r taucht darin auf*
Gibt es Werte r ∈ R , für welche diese Matrix A_r vollen Rang hat ? Wenn ja, welche ?
Zeigen Sie, falls nötig, zuerst *oben in der Fragestellung* für geeignete
1<= j <= 39.

Stell doch mal für den Kontext der Ungleichung die ganze Aufgabe rein. Dann könnte man dir besser beantworten, wie die Indizes aufzufassen sind.

Willibergi...du bist der sehr nett und du schaust dir immer meine Fragen an ... Vielen Dank! Meinst du, dass ich die Aufgabe hier reinstellen darf ?

Kann ich dir pauschal nicht sagen, aber zumindest den genauen Text abzutippen ist vermutlich kein Problem.

o.k. mache ich
3 Antworten

ist ein Matrix-Vektor-Produkt und ergibt einen 39-Vektor.
ist die j-te Komponente daraus.
Es ist wohl
die Matrix, damit ist
der Eintrag der Matrix A_r in Zeile i und Spalte j. In der Ungleichung steht auch nicht nur ein Index, sondern zwei, nämlich j,j, das wäre der j-te Diagonaleintrag, d.h. der Betrag sieht ausgeschrieben wie folgt aus:
bedeutet: Summiere von 1 bis n, aber lasse den j-ten Summanden aus. Zum Beispiel ist
die Summe über k von 1 bis 4 ohne den zweiten Summanden 2.
Zum Beweis zwei Ideen:
- Das kanonische Verfahren um zu zeigen, dass eine Matrix nicht vollen Rang hat, ist die Matrix so umzuformen, dass eine Nullzeile entsteht.
- Eine andere Möglichkeit wäre die Berechnung der Determinante. Die könnte man mit induktiver Anwendung des Laplace'schen Entwicklungssatzes aufgrund der vielen Nullen vermutlich gut berechnen.
Zur Ungleichung:
In der Regel fährt man in solchen Situationen gut damit, die Ungleichung einfach mal mit einem Wert zu berechnen und sich in jedem Schritt zu überlegen, wie dieser allgemein aussehen würde, um ein Gefühl dafür zu bekommen, warum die Ungleichung stimmt. Der Rest ist dann meist nur formalisieren (hier könnte man die Ungleichung aber auch „sehen“).
Zum Überlegen:
- Links steht der der Betrag der j-ten Komponente des Matrix-Vektor-Produkts. Was ist das genau? Was im Fall der gegebenen Matrix A_r?
- Was bedeutet die Summe rechts? Tipp: Sie ähnelt sehr der linken Seite.
Im Grunde ist das "Draufkommen" auf die Beweisidee hier ein bisschen Rumrechnerei. Verstehe die Ungleichung und überlege dir, was sie dir über den Rang der Matrix sagt. Stelle dann eine Vermutung auf und überlege dir, welches Beweisverfahren sinnvoll erscheint (d.h. was mit der Ungleichung jetzt einfacher ist: Umformen oder die Determinante berechnen?).




In der Summe ist noch ein n als Endwert, soll das jetzt für den Allgemeinfall gelten ?
Ich verstehe nicht, wie ein 39-dimensionaler Vektor aus einem Matrix-Vektor-Produkt rauskommt. Vielen Dank im Voraus für die Antwort, Willi ;)

Dass das n nicht eingeführt wurde, ist unsauber, aber das einzige, was Sinn ergibt, wäre in dem Fall n = 39 (bzw. vermutlich ist es einfacher, die Aussage allgemein für n x n Matrizen zu zeigen, sodass die 39 dabei irrelevant sind).
A_r ist eine 39x39-Matrix, x ist ein 39-dimensionaler Vektor. Damit ist A_r * x ebenfalls ein 39-dimensionaler Vektor. Ist es jetzt klarer?

Könntest du mir bitte vielleicht eine Rechnung als Beispiel aufschreiben. Irgendwie kann ich es mir nicht vorstellen. Aber Vielen lieben Dank für deine Antworten

Ich kann also beliebige Werte für x und j einsetzen, oder ?

Das ist das normale Matrix-Vektor-Produkt: http://mathb.in/48524

Nein, du sollst die Aussage für beliebige x und beliebige j zeigen. D.h. du nimmst dir ein beliebiges x und ein beliebiges j und zeigst dann die Ungleichung.

Ist MathB.in eine normale Website, oder wie hast du es aufgeschrieben ?

Ja, mathb.in ist quasi eine Website zum Formeln teilen ;-)

Ich vermute, das ganze soll auf die Gerschgorin-Kreise hinauslaufen, das würde auch zum Hinweis mit der Ungleichung passen:
https://de.wikipedia.org/wiki/Gerschgorin-Kreis
Oder besser, gleich mit Beweis,
https://en.wikipedia.org/wiki/Gershgorin_circle_theorem
Das sind Kreise mit Mittelpunkt a(i,i) und Radius = Summe der Beträge |a(i,j)| für j ungleich i. (Zeilensumme ohne das Diagonalelement.)
Alle Eigenwerte liegen in diesen Kreisen.
In der gegebenen Matrix sind die Mittelpunkte aufgrund der Fakultäten ja riesig, und die Radien im Vergleich dazu eher nicht. Wenn wir das formal nachweisen, dann haben wir nur Kreise, die nicht die Null enthalten, und dann ist 0 kein Eigenwert und die Matrix hat maximalen Rang.
Wir können also überprüfen, ob
(j=1) 2r + 1 < 2 + 4! + r^2, d.h. 0 < 4! + (r-1)^2, das gilt für alle r
(j=39) 2^42 < 2 + 42! + r^2, das gilt für alle r
(j=2...38) 2^j + 2r + 1 < 2 + j! + r^2, d.h. 2^j < j! + (r-1)^2
Hier hat man nur für kleine j Probleme:
j = 2: r darf nicht im Intervall 1-Wurzel(2), 1+Wurzel(2) liegen
j = 3: r darf nicht im Intervall 1-Wurzel(2), 1+Wurzel(2) liegen
j >= 4: die Ungleichung gilt für alle r, wegen 2^j < j!
Insgesamt hat man für r ausserhalb des genannten Intervalls maximalen Rang.

Vielen lieben Dank, wie bist du auf das Intervall 1-Wurzel(2), 1+Wurzel(2) gekommen, ich komme darauf, dass es für alle r Element R gilt
für j = 2 gilt: 2r+1+2^5 < 2+5!+r^2
-> 0 < 88 +(r-1)^2
und das gilt doch für alle r Element R, oder etwa nicht ?

Du hast recht, ich habe ein "+3" vergessen, muss also prüfen , dass
2^(j+3) < (j+3)! + (r-1)^2
Und das gilt, wie du richtig sagst, immer.

für j = 3 müsste es auch für alle r Element R gelten, oder ?

Damit es kein Durcheinander gibt:
Für j > 1 muss man prüfen, dass 2^(j+3) < (j+3)! + (r-1)^2
In meiner Antwort hatte ich bei den Fällen j=2 und =3 ein "+3" vergessen. Wenn man das hinzu nimmt, dann ist die Bedingung für alle r erfüllt.

Wieso "j +3" du zählst einfach alle Beträge der Koeffizienten einer Zeile außer das Diagonalelement zusammen. und das muss kleiner als das diagonalelement sein
also so: für j = 2 gilt: 2r+1+2^5 < 2+5!+r^2, oder ?
Und dann muss man einfach einen Bereich für r einschränken hier gibts keine Schranke, also gilt die ungleichung für alle r Element R


es kommt für j = 2 die Zahl 5 raus, warum aber das (sry ich kapier dieses j +3 nicht ;) )?

Eine Frage noch, also hat doch die Matrix für alle r Element R vollen Rang, oder ?

Ja, voller Rang. ich muss dafür alle Zeilen prüfen, und damit ich eine allgemeine Formel dafür habe, nehme ich j als Parameter für die Zeile. Dann schreibe ich die Einträge in Zeile j als Formel von j. Dabei habe ich bei meiner Antwort ein "+3" vergessen, in Zeile 2 steht ja z.B. gleich in der ersten Spalte 2^5 = 2^(j+3). Damit wollen wir dieses Kapitel jetzt abschliessen.

in einer Matrix ist a j,k das Element zur Zeile j und Spalte k.
k ungleich j in der Summe bedeutet, dass das Element a j,j beim Summieren weggelassen wird.

Vielen Dank Willi ;-)