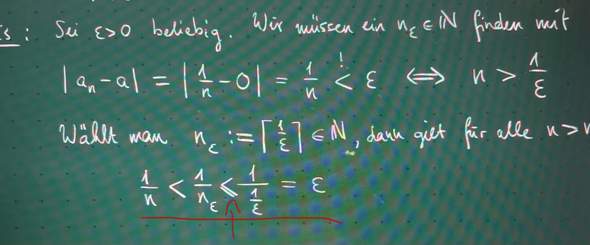Mathematik, Informatik & Logik

Zu beweisen

Wenn ich das mithilfe der Induktion über n machen möchte (erstes Element von N ist 1) und dadurch beim Induktionsanfang herauskommt, dass 1+x=1+x

Aber wenn ich jetzt den Induktionsschritt mache, und dieselbe aussage für n+1 beweisen möchte, komme ich statt größer gleich auf echt größer.

Aber damit habe ich doch nicht die Aussage für n+1 gezeigt? Denn für n+1 ist sie ja echt gleich.

kann ich jetzt sagen: da für n=1 die gleichheit gilt und für n+1 die ungleichheit, dass somit folgt, dass (1+x)^n >= 1+nx, weil man die gleichheit und die echt größer hat?

Hallo, ich habe heute eine Mathe Arbeit zum Thema 1. - 2. Strahlensatz geschrieben, die letzte Aufgabe war die auf dem Bild ( Meine Künstlerische Fähigkeit ist am pc stark begrenzt ). Ich habe in der Klasse so rumgefragt und ALLE haben verschiedene Antworten, ich wollte jetzt mal Fragen wie man diese Aufgabe denn rechnet und was die Lösung wäre.
LG Gabriel

Also zum Beispiel habe ich die Brüche 1/3 1/4 und 1/7 ich muss die alle addieren. Aber die Brüche haben keinen gemeinsamen nenner. Wie funktioniert das?

Ich habe die Bedingungen aufgestellt und muss jetzt die Gleichungen nach den Variablen auflösen. Wie kann man das machen?

Aufgabe; Medikamentenkonzentration

Um eine möglichst lange Wirkungsdauer von Medikamenten zu erreichen, werden in der Medizin spezielle Tabletten oder Kapseln genutzt, die den Wirkstoff sehr langsam freisetzen. Bei der Entwicklung eines sol- chen Medikaments ist es sinnvoll, die Konzentration eines Medikamentes im Blutplasma (Blutflüssigkeit) zu untersuchen.

Die Konzentration des Medikamentes wird dabei in Milligramm pro Liter angegeben (mg/l).

a) Über ein neu entwickeltes Medikament ist bekannt, dass es zu Beginn der Einnahme nicht nachweisbar ist, d.h. die Konzentration im Blutplasma beträgt 0 mg/l. Zwei Stunden nach der Einnahme ist die Kon- zentration mit 5,3 mg/l maximal. Drei Stunden nach der Einnahme beträgt die Konzentration im Blut 4,5 mg/l.

Bestimmen Sie eine ganzrationale Funktion f dritten Grades, die den dargestellten Sachverhalt be- schreibt. gibt dabei die Zeit in Stunden nach der Einnahme an und f(r) die Konzentration des Medikamentes im Blutplasma in mg/l. Eine anschließende Überprüfung, ob die bestimmte Funktion f die obigen Angaben erfüllt, ist nicht notwendig.

Meine Rechnung;

Die allgemeine Volumen Formel (V=a•b•c) vom Quader würde doch dann nicht mehr funktionieren, weil die Grundfläche oben wo die Halbkugel drauf sitzt nicht mehr komplett ist oder? Oder hat die Kugel nur ein Einfluss auf die Oberfläche und das Volumen kann man noch ganz normal berechnen?

Guten Abend Sportsfreunde,

in der Analysis haben wir diese Aufgaben erhalten:

Beweisen Sie: Jedes nichtleere und beschränkte Intervall in ℝ kann auch dargestellt werden als Vereinigung von abzählbar vielen abgeschlossenen Intervallen der Form I = [a, b] mit a, b ∈ ℝ.

Jedoch habe ich keinerlei Ideen/Ansätze für die Aufgabe. Ich weiß, wie das Ergebnis aussehen könnte, da ich mir unter der Vereinigung abgeschlossener Intervalle etwas vorstellen kann. Eigentlich kann ich mit allen Begriffen etwas anfangen, aber wie soll man hier starten? Hat jemand eine Idee?

Ich bin dankbar für jede Hilfe. Habt einen angenehmen Abend:)

Heyy, ich stehe gerade voll auf dem Schlauch.

 kann ich das einfach * 2 rechnen?

Also:

 oder wie muss ich das lösen?

wie wurde es von -2/3 zu pi/3

Hey, ich lerne gerade Mathe und bin bei einer Aufgabe am verzweifeln… Vielleicht könnte jemand von euch mir eine Aufgabe mitsamt des Rechenweges vorrechnen, sodass ich daran die folgenden Aufgaben lösen könnte?

Ich wäre euch sehr dankbar ;)

LG Luzie822🙃

Das wären die Nummer 2,3&4.

Hey Gute Frage Nutzer:) Wir haben diese Aufgabe im Unterricht gemacht( siehe Bild). Die Wahrscheinlichkeit war bei Junge und Mädchen 0,3118. Mein Lehrer hat noch eine Zusatzaufgabe gestellt die wäre: berechne die Wahrscheinlichkeit, dass die Familie zwei oder weniger jungen hat. P(x<2)= P(x=2)+P(x=1)+P(x=0) . Ich weiß nicht genau wie ich vorgehen soll:/ Ich bitte um Hilfe🙏🏼

Wie im Spiel detroit, bekomme a Human.

Kara der Roboter hat ihren Meister, befehlen widersetzt , da er betrunken, gewalttätig seine eigene kleine Tochter ermorden wollte.

Würde das künstliche Intelligenz wirklich zulassen, nur weil Sie keine Gefühle haben.

Bei meiner Aufgabe im Mathebuch soll ich zwei Ebenen auf die gemeinsame Lage prüfen. Nun wenn man sie gleichsetzt und in ein LGS bringt entsteht das linke der beiden. Nun frage ich mich ob es überhaupt möglich ist dies in die rechte Form zu bringen. Und wenn ja wie? Vielen Dank für Hilfe

Hallo. Ich habe hier eine Frage an die Mathelehrer und Börsenmakler der Nation:

Angenommen, ich blicke auf den Kursverlauf einer Aktie.

Wie berechne ich den größtmöglichen Gewinn, der innerhalb eines bestimmten Zeitraums möglich gewesen wäre?

Das höchste Hoch minus das tiefste Tief im gewählten Zeitraum, scheint mir nicht der richtige Rechenweg zu sein, da ja auch zwischen diesen Werten Käufe und Verkäufe von Aktien stattgefunden haben können, die wiederrum Geld für weitere Aktienkäufe ermöglicht haben.

Vielen Dank für alles, was mich weiterbringt :)

Verstehe das Endergebnis irgendwie nicht, also 1/n < 1/n epsilon schon, aber das danach nicht

Aufleitung von 1/x*2+16

Warum subsitieren wir mit x = 1/4s statt x=4s

Hi!

Also ich habe ein Problem bzgl. Binärzahlen.

Wenn ich als Beispiel die -77 (dezimalzahl) nehme und diese in einer Bitlänge von 8 in sowohl eine Binärzahl, als auch in ein Zweierkomplement umwandeln will gehe ich folgendermaßen vor:
Die -77 drehe ich für mich in die 77 um.
Daraus ergibt sich für mich die Binärfolge: 0100 1101.
Wenn ich diese Binärfolge in ein zweierkomplement umrechnen will, dann invertiere ich zuerst meine Binärfolge und addiere zunächst 1 drauf.
Es ergibt sich: 10110011. Laut meinem Verständnis ist das das Zweierkomplement für -77. Oder ist es das für sowohl 77 als auch für -77?

Wie mache ich das bei positiven Zahlen? Ich habe es so verstanden, dass ich die Binärfolge nicht invertiere sondern einfach auch bei einer positiven Zahl auf das Zweierkomplement übertragen kann. Stimmt das?

Danke :)