Ich persönlich finde Tuxedo-Katzen besonders niedlich :)

Also als wir das Dramenfragment in der Schule gelesen haben, sollten wir unter anderem die Schuldfähigkeit Woyzecks diskutieren, aber auch darüber, inwiefern Marie möglicherweise "Schuld" an ihrem eigenen Tod trägt...

Guten Abend,

der beste Ansatz für Aufgaben dieser Art ist es, sich zunächst einmal alle relevanten Informationen aus der Aufgabenstellung herauszuschreiben und auf Grundlage dessen ein Baumdiagramm zur Berechnung der Wahrscheinlichkeiten anzufertigen:

Es ist bekannt, dass die Klasse insgesamt 25 Schüler/innen umfasst, von denen 5 die Hausaufgaben nicht erledigt haben.

Der Lehrer wählt insgesamt zwei mal zufällig einen Schüler aus, dieser hat die Hausaufgaben entweder erledigt oder nicht erledigt.

Daher gibt es an jeder Abzweigung des Baumdiagrammes zwei Äste - der eine steht für die Wahrscheinlichkeit, dass der Lehrer jemanden auswählt, der die Aufgaben nicht gemacht hat, und der andere für die Wahrscheinlichkeit, dass der Lehrer jemanden auswählt, der die Aufgaben gemacht hat.

Wenn man nun ausschließt, dass der gleiche Schüler zweimal ausgewählt wird, sind es beim ersten Mal insgesamt 25 Schüler, aus denen der Lehrer auswählt, und beim zweiten Mal 24 Schüler.

Wenn der Lehrer beim ersten Mal einen der 5 Schüler auswählt, die die Hausaufgaben nicht erledigt haben, so gibt es beim zweiten Mal nur noch 4 Schüler mit nicht gemachten Hausaufgaben, die vom Lehrer ausgewählt werden könnten.

Das gleiche gilt natürlich auch andersherum: Wenn der Lehrer beim ersten Mal einen der 20 Schüler auswählt, die die Hausaufgaben gemacht haben, so sind es beim zweiten Mal nur noch 19 Schüler mit erledigten Hausaufgaben, die in Frage kämen.

Daraus ergibt sich dann das folgende Baumdiagramm:

Mithilfe dieses Baumdiagrammes lassen sich nun die Wahrscheinlichkeiten der in der Aufgabe genannten Ergebnisse berechnen:

E1: Beide Schüler haben keine Hausaufgaben

Wenn Du die Wahrscheinlichkeit ausrechnen möchtest, mit der beide der ausgewählten Schüler ihre Hausaufgaben nicht erledigt haben, musst Du an den Gabelungen im Baumdiagramm zweimal dem Ast zu den nicht gemachten Hausaufgaben folgen und die daran stehenden Wahrscheinlichkeiten miteinander multiplizieren.

Im Baumdiagramm wäre das der folgende Weg:

Du erhältst also die Brüche 5/25 und 4/24, die miteinander multipliziert werden müssen.

5/25 • 4/24 = 20/600 = 1/30 ≈ 0,03333

Die Wahrscheinlichkeit, dass beide Schüler keine Hausaufgaben haben, liegt also bei etwa 3,33%.

E2: Einer der beiden Schüler hat keine Hausaufgaben gemacht

Bei dieser Aufgabe musst Du auf die gleiche Weise wie bei der ersten Aufgabe vorgehen. Dieses Mal gibt es jedoch zwei Wege, mit denen die Bedingungen der Aufgabenstellung erfüllt werden:

Daher musst du folgende Rechnung aufstellen:

(5/25 • 20/24) + (20/25 • 5/24) = 100/600 + 100/600 = 200/600 = 1/3 ≈ 0,3333

Die Wahrscheinlichkeit, dass einer der beiden Schüler keine Hausaufgaben gemacht hat, liegt also bei etwa 33,33%.

E3: Beide Schüler haben die Hausaufgaben gemachten

Bei dieser Aufgabe musst Du wieder auf die gleiche Weise wie bei den davorigen Aufgaben vorgehen. Der Weg im Baumdiagramm sieht dabei folgendermaßen aus:

Daraus ergibt sich die Rechnung:

20/25 • 19/24 = 380/600 ≈ 0,6333

Die Wahrscheinlich, dass beide Schüler die Hausaufgaben gemacht haben, liegt also bei etwa 63,33%.

Ich hoffe, das war soweit alles verständlich!

Hallo zusammen,

ich habe hier einmal ein paar Ideen für ähnlich klingende Namen aufgeschrieben:

• Lina, Regina, Sarina, Ina, Bettina, Sina, Tina, Felina, Mina
• Mara, Tara, Clara, Sarah, Lara, Chiara, Zara
• Mia, Pia, Sofia, Maria, Lia, Sia, Tia
• Anneliese, Anna, Anne, Andrea, Annabelle, Annalena, Ann-Kathrin

Ich hoffe, ich konnte damit weiterhelfen - Viel Erfolg mit dem Theaterstück!

Also mir haben im Alter von 6 Jahren besonders folgende Dinge Freude bereitet:

• das Spielen mit Lego oder Playmobil🏠
• Puzzles und Rätsel🧩
• das Malen mit bunten Stiften auf Papier oder mit Kreide auf der Straße🎨
• das Erforschen der Natur (zum Beispiel bei Ausflügen in den Wald)🌿
• das Lesen von Bilderbüchern mit fantasievollen Geschichten📚
• das Verkleiden an Karneval🎉
• Verabredungen mit Freunden👥
• Kochen und Backen🍰
• das Eisessen im Sommer🍦
• Musik🎧
• Ausflüge ins Schwimmbad oder den Zoo🐾
• Sport (sportliche Betätigung) mit Freunden im Verein⚽️

Besonders mochte ich damals auch alles, was mit Tieren oder der Natur zu tun hatte!

People don‘t change, they’ve just never been what you thought they were.

Ich hoffe, das ist soweit verständlich!

Hallo,

ich habe hier einmal einen Weg aufgeschrieben, wie Du die Aufgabe lösen kannst:

Du weißt dank der Aufgabenstellung, dass drei Mal eine Kugel aus der Urne gezogen wird und dass diese nicht wieder zurückgelegt wird, die Anzahl der Kugeln mit jedem Ziehen also kleiner wird.

Auf dem Bild ist zu erkennen, dass sich ganz zu Beginn 7 Kugeln in der Urne befinden, davon sind 5 mit dem Buchstaben Z und 2 mit dem Buchstaben X beschriftet.

Nun kannst Du auf Grundlage dessen ein Baumdiagramm für die Aufgabe erstellen, mithilfe dessen Du dann die Wahrscheinlichkeiten für bestimmte Ergebnisse (zum Beispiel Z-Z-X) berechnen kannst.

Ich habe hier einmal ein Baumdiagramm zu der Aufgabe erstellt, das Du dir ansehen kannst:

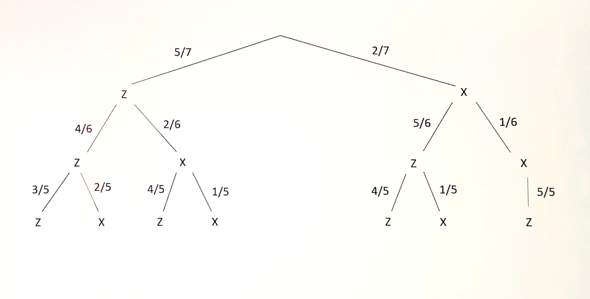
Da es in der Urne nur zwei verschiedene Arten von Kugeln (entweder X oder Z) gibt, gibt es pro Zug auch immer nur zwei unterschiedliche Äste.

Beim ersten Zug sind noch 7 Kugeln in der Urne, 5 mit der Aufschrift Z und 2 mit der Aufschrift X.

Daher steht auf dem oberen Ast, der zum Buchstaben Z führt der Bruch 5/7 (also die Wahrscheinlichkeit, ein Z zu ziehen) und auf dem Ast, der zum Buchstaben X führt, der Bruch 2/7 (also die Wahrscheinlichkeit, ein X zu ziehen).

Beim zweiten Zug befinden sich dann folglich nicht mehr 7, sondern nur noch 6 Kugeln in der Urne (eine wurde ja schon im ersten Zug herausgenommen), was man auch an den Wahrscheinlichkeiten an den Ästen erkennt. Nun steht keine 7 mehr, sondern eine 6 im Nenner des Bruches.

Wenn im ersten Zug ein Z gezogen wurde, so gibt es in der Urne beim zweiten Zug auch ein Z weniger als zu Beginn. Das gleiche gilt für den Buchstaben X. Wurde im ersten Zug eine der beiden Kugeln mit der Aufschrift X gezogen, ist beim zweiten Zug nur noch ein X in der Urne.

Das gleiche gilt auch für den dritten Zug. Wenn zum Beispiel im ersten und zweiten Zug beide Male der Buchstabe Z gezogen wurde, gibt es beim dritten Zug nur noch drei Kugeln mit dem Buchstaben Z. Deshalb steht am linken unteren Ast auch der Bruch 3/5; es sind noch 5 Kugeln in der Urne, von denen 3 mit dem Buchstaben Z beschriftet sind.

Auf der rechten unteren Seite des Baumdiagramms erkennst Du zum Beispiel auch, dass es nur einen Ast gibt, an dem die Wahrscheinlichkeit 5/5 (also 100%) steht. Das liegt daran, dass es von Anfang an nur zwei Kugeln mit dem Buchstaben X gibt. Wenn beide dieser Kugeln schon in den ersten beiden Zügen gezogen werden, kann beim dritten Zug folglich nur noch ein Z gezogen werden, weil keine Kugel mit dem Buchstaben X mehr in der Urne ist.

Wenn Du nun die Wahrscheinlichkeit für ein bestimmtes Ergebnis berechnen möchtest, musst du lediglich den entsprechenden Ästen des Baumdiagrammes folgen und die einzelnen Wahrscheinlichkeiten multiplizieren.

Lösung der Teilaufgaben a-c

In der ersten Aufgabe soll die Wahrscheinlichkeit der Zugfolge XXZ berechnet werden, also musst Du im Baumdiagramm an der ersten und zweiten Gabelung zum X und an der dritten Gabelung zum Z gehen.

Ich habe dir den Weg hier einmal in grün markiert:

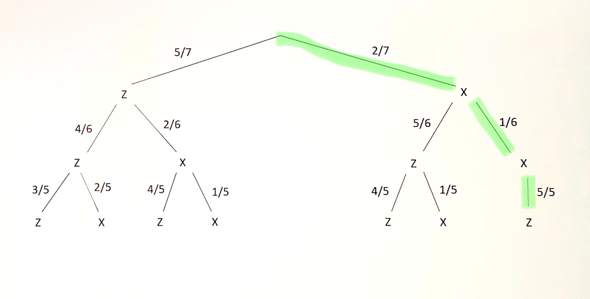
An den entsprechenden Ästen findest Du die Brüche 2/7, 1/6 und 5/5, die miteinander multipliziert werden müssen:

2/7 • 1/6 • 5/5 = 1/21

Die Wahrscheinlichkeit für die Ziehfolge XXZ beträgt also etwa 4,76%.

Bei der zweiten Aufgabe verfährst du dann auf die gleiche Weise und folgst dem Ast zu X, zu Z und dann zu X:

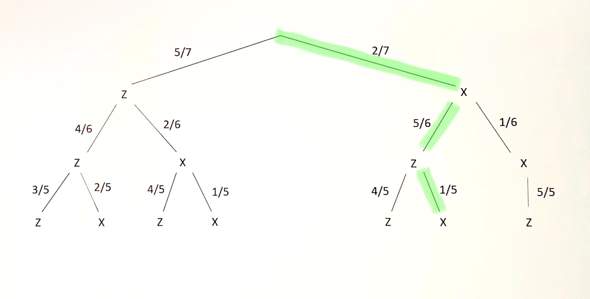
Auf diese Weise erhältst du die Brüche 2/7, 5/6 und 1/5, die Du wieder miteinander multiplizierst:

2/7 • 5/6 • 1/5 = 10/210

Die Wahrscheinlichkeit der Ziehfolge XZX beträgt also etwa 4,76%.

Die dritte Aufgabe ist dann eine Falle, weil nicht drei Mal der Buchstabe X gezogen werden kann, wenn es ihn nur zweimal gibt und die Kugeln nach dem Ziehen noch wieder in die Urne zurückgelegt werden. Daher ist die Ziehfolge XXX unmöglich.

Das war dann auch meine Erklärung der Aufgabe, ich hoffe, es war soweit verständlich!

Also Meiner Meinung nach, ist ein Date im Wald oder generell in der Natur immer eine schöne Idee💚

Man kann in Ruhe spazieren gehen oder auf einer Wiese/Lichtung im Grünen etwas picknicken!

Gerade im Frühling/Frühsommer lohnt es sich, mal draußen in der Natur spazieren zu gehen, wenn alles blüht🌷

Also ich persönlich hatte im Internet immer sehr positive Rezensionen zum Film Thor - Love and Thunder gelesen und war daher auch davon ausgegangen, dass dieser von seiner Art her ähnlich wie die vorherigen Thor Filme sein würde.

Entsprechend groß war meine Enttäuschung, als ich feststellen musste, dass dieser Film in seiner Atmosphäre und Handlung nicht mehr wirklich mit den älteren Filmen zu tun hatte.

Der Film erschien mir an vielen Stellen eher wie eine Art Parodie:

Thor, der auf einem Besen durch die Gegend fliegt und ein paar Stofftiere in Raumschiffen vernichtet,

eine Schar von Kindern, die mit Thors Kräften und ein paar Kuscheltieren gegen Bösewichte kämpfen,

schreiende Ziegen, die ein fliegendes Vergnügungspark-Schiff auf einer Brücke durch die Galaxie ziehen

und eine Eifersuchtstragödie zwischen einem Hammer und einer Wurfaxt.

Ich persönlich fand das sehr schade, da ich das Gefühl hatte, dass der ganze Film krampfhaft ins Lächerliche gezogen war und die eigentliche Story darunter litt.

Natürlich hatte ich mir keinen vollkommen ernsten und fantasielosen Marvel Film erhofft, aber der überzogene Humor und die abgedrehte Handlung waren mir einfach zu viel.

Aber das ist in jedem Falle auch nur meine persönliche Meinung - vielleicht hat der Film anderen ja auch besser gefallen!

Also mir persönlich hat es sehr geholfen, eine Pause von Social Media einzulegen, da ich erst im Nachhinein wirklich erkannt habe, wie viel Zeit ich bis zu diesem Zeitpunkt jeden Tag im Internet verbracht hatte.

Ohne Social Media blieb mir viel mehr Zeit, um anderen Beschäftigung nachzugehen und auch die Konzentration (zum Beispiel beim Lernen) fiel mir deutlich leichter, da ich nicht mehr durch Benachrichtigungen oder Neuigkeiten auf Social Media Plattformen abgelenkt wurde.

Außerdem tut es meiner Meinung nach gut, sich auch einmal von dem ganzen Fluss an Informationen, Neuigkeiten, Unterhaltung, usw. zurückzuziehen und sich auf sein reales Umfeld zu konzentrieren.

Hallo,

ich kenne mich leider nicht ganz so gut mit dem Thema aus, aber ich habe folgende Website gefunden, auf der das Ganze recht anschaulich erklärt ist:

https://healthyhappy.de/wieviel-kalorien-ein-kilo-fett/

Vielleicht hilft dir das ja weiter!

"Wenn ich allein bin, bin ich am wenigsten allein"

- Marcus Tullius Cicero -

Hallo,

ich habe Dir hier einmal einen Rechenweg beschrieben, wie du die Aufgabe lösen kannst:

Bei dieser Aufgaben solltest Du zunächst einmal eine Gleichung aus den Informationen aus dem Text aufstellen, um das Ergebnis ausrechnen zu können.

Du weißt aufgrund der Aufgabenstellung, dass eine Menge von 30g einen Eiweißanteil von 23g enthält.

Daher schreibst Du:

23/30 = x/40

• die 23/30 stehen für die Menge an Eiweiß pro 30g-Portion
• das x steht als Variable für die Menge an Eiweiß, die bei einer 40g-Portion den gleichen Anteil ausmacht

Da du wissen möchtest, wie viel Eiweiß in der 40g-Portion enthalten ist, musst Du die Gleichung zunächst nach x auflösen. Dies kannst Du tun, indem Du auf beiden Seiten der Gleichung mit 40 multiplizierst.

Du erhältst die Gleichung:

23/30 • 40 = x

Um x auszurechnen, musst Du jetzt nur noch die 23 im Zähler mit 40 multiplizieren; die Gleichung sieht dann folgendermaßen aus:

920/30 = x

Wenn Du nun den Bruch kürzt, erhältst Du ein Ergebnis von 92/3, also ungefähr 30,67.

Du weißt also:

30,67 = x

Da die Variable x für die Menge an Eiweiß pro 40g steht, weißt Du nun also, dass in einer 40g Portion etwa 30,67g Eiweiß enthalten sind.

Ich hoffe, ich konnte mit meiner Antwort weiterhelfen!

Hallo,

wenn Du mathematische Terme ausrechnen möchtest, solltest du die folgende Reihenfolge beachten:

1. Klammern - Wenn in dem Term eine Rechnung in Klammern steht, muss diese als allererstes ausgerechnet werden.
2. Potenzen - Beinhaltet der zu lösende Term Potenzen, müssen diese nach den Klammern als erstes berechnet werden.
3. Punktrechnung - Multiplikation und Division müssen noch vor den Strichrechnungen durchgeführt werden.
4. Strichrechnung - Addition und Subtraktion werden als Letztes durchgeführt.
5. Den Term von links nach rechts ausrechnen.

Nach dieser Reihenfolge kannst du nun also auch deine Rechnung lösen:

9 - 3 ÷ 1/3 + 1

Da der Term keine Klammern oder Potenzen beinhaltet, suchst Du zunächst nach Punktrechnungen, also Multiplikationen oder Divisionen. Im gegebenen Term erkennst du, dass die 3 durch die 1/3 geteilt wird, also eine Division vorliegt.

Wenn eine Zahl durch einen Bruch, wie zum Beispiel 1/3 geteilt werden soll, musst du sie mit dem Kehrwert des Bruches, in diesem Falle also mit 3/1 multiplizieren. Da 3/1 = 3 sind, erhältst du also:

9 - 3 x 3 + 1

bzw.

9 - 9 + 1

da 3 x 3 = 9 ist.

Nun besteht dein Term nur noch aus Strichrechnungen, also Additionen und Subtraktionen, wodurch du ihn einfach von links nach rechts ausrechnen kannst.

9 - 9 ergibt 0

0 + 1 ergibt 1

Die Lösung des gegebenen Terms ist also 1.

Ich hoffe, ich konnte Dir damit weiterhelfen!

Hallo,

ich habe hier mal ein paar Mädchennamen mit doppeltem S in der Mitte aufgeschrieben, die mir eingefallen sind:

• Alessa
• Alessia
• Alissa
• Cassandra
• Cassie
• Chrissy
• Clarissa
• Clarisse
• Dorisse
• Felisse
• Jessy
• Kassandra
• Kassie
• Larissa
• Lissa
• Lissy
• Loussia
• Melissa
• Missie
• Nissa
• Nessie
• Tessa
• Tessie
• Vanessa

Ich hoffe, ich konnte damit weiterhelfen!

Ein Tetraeder hat insgesamt 4 Spitzen, das bedeutet, dass die Zahlen 1-4 gewürfelt werden können. Da beim Tetraeder alle Flächen gleich groß sind, liegt die Wahrscheinlichkeit, eine bestimmte Zahl zu würfeln bei 1/4. Mit diesem Wissen lassen sich nun auch die Aufgaben lösen:

E1: Mindestens einmal Augenzahl 1

Da zweimal gewürfelt wird und die Wahrscheinlichkeit, eine 1 zu würfeln für jeden Wurf 1/4 beträgt, lässt sich die gesamte Wahrscheinlichkeit folgendermaßen ausrechnen:

(1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) = 7/16 ≈ 43,75%

Es wird sieben mal (1/4 • 1/4) gerechnet, da es sieben Mögliche Kombinationen gibt, in den zwei Würfen mindestens eine 1 zu würfeln:

1 + 1, 1 + 2, 1 + 3, 1 + 4, 2 + 1, 3 + 1, 4 + 1

Die Wahrscheinlichkeit, bei mindestens einem der beiden Würfe eine 1 zu würfeln, liegt also bei etwa 43,75%.

E2: Beim zweiten Wurf Augenzahl 1

In diesem Falle gibt es vier mögliche Kombinationen, mit denen das gewünschte Ergebnis erzielt werden kann:

1 + 1, 2 + 1, 3 + 1, 4 + 1

Die Wahrscheinlichkeit lässt sich also folgendermaßen berechnen:

(1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) = 4/16 = 1/4 = 25%

Die Wahrscheinlichkeit, beim zweiten Wurf eine 1 zu würfeln, liegt also bei 25%.

E3: Nur beim zweiten Wurf Augenzahl 1

In diesem Falle gibt es nur drei mögliche Kombinationen, mit denen die Bedingungen erfüllt werden kann:

2 + 1, 3 + 1, 4 + 1

Daher lässt sich die Wahrscheinlichkeit folgendermaßen berechnen:

(1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) = 3/16 ≈ 18,75%

Die Wahrscheinlichkeit, nur beim zweiten Wurf eine 1 zu würfeln, liegt also bei etwa 18,75%.

E4: Nur ungerade Augenzahlen

In diesem Falle gibt es drei mögliche Kombinationen, mit denen in beiden Würfen nur ungerade Zahlen gewürfelt werden:

1 + 1, 1 + 3, 3 + 1, 3 + 3

Die Wahrscheinlich kann also folgendermaßen berechnet werden:

(1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) = 4/16 = 1/4 = 25%

Die Wahrscheinlichkeit, bei beiden Würfen ungerade Zahlen zu würfeln, liegt also bei 25%.

E5: Eine gerade, eine ungerade Augenzahl

In diesem Falle gibt es acht mögliche Kombinationen, mit denen das gewünschte Ergebnis erzielt werden kann:

1 + 2, 1 + 4, 3 + 2, 3 + 4, 2 + 1, 2 + 3, 4 + 1, 4 + 3

Somit lässt sich die Wahrscheinlichkeit folgendermaßen berechnen:

(1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) + (1/4 • 1/4) = 8/16 = 1/2 = 50%

Die Wahrscheinlichkeit, bei beiden Würfen eine gerade und eine ungerade Zahl zu würfeln, liegt also bei 50%.

E6: Augensumme 3

Es gibt insgesamt zwei verschiedene Möglichkeiten, um mit zwei Würfen die Summe 3 zu erzielen:

1 + 2, 2 + 1

Daher kann man die Wahrscheinlichkeit folgendermaßen berechnen:

(1/4 • 1/4) + (1/4 • 1/4) = 2/16 = 1/8 = 12,5%

Die Wahrscheinlichkeit, mit zwei Würfen die Summe 3 zu erzielen, liegt also bei 12,5%.

Ich hoffe, ich konnte durch meine Antwort weiterhelfen!

Also ich finde es überhaupt nicht komisch, sich mit 16 immer noch mit solchen Dinge zu beschäftigen. Meiner Meinung nach kann man Filme und Bücher ein Leben lang toll finden - unabhängig vom Alter.

Warum solltest du dich nicht von spannenden Geschichten mitreißen und inspirieren lassen, wenn es dich motiviert und dir Freude bereitet? Es ist doch etwas Schönes, sich auch mal fantasievollen Dingen zu widmen, das geht nur leider im Alter den meisten Menschen verloren.

Schade finde ich es nur, dass das heutzutage so herablassend betrachtet wird - es hat doch immerhin jeder seine ganz eigenen Interessen und das ist auch gut so!

Ich bin der Meinung, dass es wichtig ist, offen für andere Lebensweisen und Kulturen zu sein. Ein rücksichtsvoller Umgang basiert dabei meiner Ansicht nach immer auf Beidseitigkeit: Ich lasse mich auf andere Kulturen ein und bin respektvoll gegenüber fremden Gewohnheiten, möchte aber auch, dass mir mit der gleichen Offenheit und dem gleichen Maß an Respekt begegnet wird.

Was für uns vielleicht fremd und ungewohnt erscheint, gehört für andere zum alltäglichen Leben, während Dinge, die wir für normal erachten in anderen Kulturen unüblich sind.

Daher sollte man meiner Meinung nach keine Vorurteile gegenüber anderen Kulturen haben, sondern ihnen vielmehr mit Interesse begegnen. Denn es ist eine gute Gelegenheit, seinen eigenen Horizont zu erweitern und etwas Neues dazuzulernen.

Eine wirklich gelungene Zeichnung - Er wird sich sicherlich darüber freuen!

Guten Abend,

ich habe Dir hier einmal zwei Wege beschrieben, wie Du die Aufgabe lösen kannst. Ich hoffe, es ist soweit verständlich!

|

Bei dieser Aufgaben solltest Du zunächst einmal eine Gleichung aus den Informationen aus dem Text aufstellen, um das Ergebnis ausrechnen zu können.

Du weißt aufgrund der Aufgabenstellung, dass die Anzahl von 18 Schülern 60% der Klasse ausmacht.

Daher schreibst Du:

18 = 60/100 • x

• die 18 steht für die Anzahl der 16-jährigen Schüler/innen in der Klasse
• die 60/100 stehen für die 60% der Klasse, die 16 Jahre alt sind
• das x steht als Variable für die Gesamtzahl an Schülern in der Klasse, die ausgerechnet werden soll

Da du wissen möchtest, wie viele Schüler/innen insgesamt in der Klasse sind, musst Du die Gleichung zunächst nach x auflösen. Dies kannst du tun, indem Du auf beiden Seiten der Gleichung durch 60/100 dividierst.

Du erhältst die Gleichung:

18 : 60/100 = x

Um x zu erhalten, musst du jetzt nur noch die 18 durch die 60/100 teilen. Man teilt eine Zahl durch einen Bruch, indem man sie mit dem Kehrwert multipliziert, daher sieht deine Gleichung dann folgendermaßen aus:

18 • 100/60 = x

Wenn Du die 18 mit den 100/60 multiplizierst, erhältst du ein Ergebnis von 1800/60. Kürzt Du diesen Bruch mit 60, kommst Du auf ein Ergebnis von 30.

Du weißt also:

30 = x

Da die Variable x für die Anzahl an Schülern in der Klasse steht, weißt Du nun also, dass insgesamt 30 Schüler/innen in der 9ten Klasse sind.

|

Alternativ ließe sich diese Aufgabe auch etwas einfacher mithilfe des Dreisatzes lösen:

Du weißt dank der Aufgabenstellung, dass die 18 Schüler/innen 60% der Klasse ausmachen und möchtest wissen, wie viel 100% der Klasse sind.

18 = 60%

Wenn du beide Zahlen durch 6 dividierst, erhältst du:

3 = 10%

Nun weißt Du, dass 3 Schüler/innen 10% der Klasse ausmachen. Da du aber wissen willst, wie viel 100% der Klasse sind, multiplizierst Du das Ganze noch einmal mit 10.

Du erhältst:

30 = 100%

Auf diese Weise hast Du nun also ausgerechnet, dass insgesamt 30 Schüler/innen in der Klasse sind.
|

Ich hoffe, ich konnte dir mit meiner Antwort weiterhelfen - Viel Erfolg auch bei künftigen Matheaufgaben!