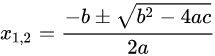Wie kann ich die Mitternachtsformel auf die allgemeine Form anwenden?
Also, wenn es geht mit einer Beispiel Aufgabe.
Thema: Quadratische Funktionen.
1 Antwort
Die allgemeine Form der Quadratischen Gleichung ist bekanntlich:
ax² + bx + c = 0
Lösung per Mitternachtsformel
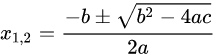
ist dann simples Einsetzen von a, b und c.
Für x1 (erste Nullstelle) rechnest du beim ± mit +, für x2 (zweite Nullstelle) entsprechend mit -.
Wenn die Diskriminante (das b² - 4ac unter der Wurzel) gleich 0 ist, dann ist logischerweise x1 = x2, es gibt also nur eine ("doppelte") Nullstelle - ein Berührpunkt mit der x-Achse. Ist die Diskriminante negativ (d.h. 4ac > b²), dann gibt es keine (reellen) Nullstellen, d.h. die Parabel schneidet die x-Achse gar nicht.
https://de.wikipedia.org/wiki/Quadratische_Gleichung#Rechenbeispiel_2