Wie funktioniert die Modrelation?
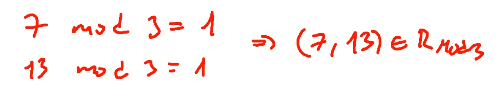
Wenn ich z. B. die Modrelation mit mod 3 auf die natürlichen Zahlen anwende, wie würden Tupel darin aussehen? Könnte jemand das als Beispiel erklären, warum sollte denn die (7,13) als Tupel in der Relation sein?
Ich ging eher davon aus, dass die Modrelation so aufgebaut ist:
(1,13)
13mod3 wäre rest 1 und der rest kommt links und die zahl rechts oder (1,7) etc.
1 Antwort
Vom Beitragsersteller als hilfreich ausgezeichnet
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik
Wichtig ist in diesem Zusammenhang die Relation der Kogruenz:
man sagt: 7 und 13 sind kongruent modulo 3, weil sie bei Division durch 3 den selben Rest haben, man schreibt z.B. 7 ≡ 13 mod 3 ........... 3 teilt die Differenz 13 - 7
(7, 13) sind dann Elemente einer Äquvalenzrelation, deren Äquivalenzklassen Restklassen heißen, also (7, 13) ∈ ~
siehe: